题目内容
18.解方程:(1)$\frac{x-2}{x+2}$-$\frac{16}{{x}^{2}-4}$=$\frac{x+2}{x-2}$;
(2)$\frac{4}{{x}^{2}-1}$+$\frac{x+2}{1-x}$=-1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:(x-2)2-16=(x+2)2,
整理得:8x=-16,
解得:x=-2,
经检验x=-2是增根,分式方程无解;
(2)去分母得:4-(x+2)(x+1)=-x2+1,即4-x2-3x-2=-x2+1,
移项合并得:3x=1,
解得:x=$\frac{1}{3}$,
经检验x=$\frac{1}{3}$是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目

 在△ABC中,∠C=∠ABC,AE∥BC,BE平分∠ABC,则下列结论中一定成立的是①②④(把所有正确结论的序号都填在横线上).
在△ABC中,∠C=∠ABC,AE∥BC,BE平分∠ABC,则下列结论中一定成立的是①②④(把所有正确结论的序号都填在横线上). 如图,已知∠AOB=60°,点P是OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则ON=5cm.
如图,已知∠AOB=60°,点P是OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则ON=5cm.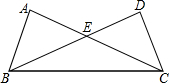 如图,在Rt△ABC和Rt△BCD中,∠A=∠D=90°,AB=CD=4,BC=$4\sqrt{5}$,△BCE的面积=10.
如图,在Rt△ABC和Rt△BCD中,∠A=∠D=90°,AB=CD=4,BC=$4\sqrt{5}$,△BCE的面积=10.