题目内容
11. 如图,三角形ABC的面积为8cm2,点D、E分别在边BC、AC上,BE交AD于点F,若BD=CD,AF=3FD,则三角形ABD的面积是4cm2,三角形DEF的面积是0.6cm2.
如图,三角形ABC的面积为8cm2,点D、E分别在边BC、AC上,BE交AD于点F,若BD=CD,AF=3FD,则三角形ABD的面积是4cm2,三角形DEF的面积是0.6cm2.
分析 根据三角形的面积S=底×高÷2,结合边的比例关系,就能找到各三角形面积的关系,结合三角形ABC的面积为8cm2,即可得出结论.
解答 解:连接DE,如图所示:
∵BD=CD,
∴在△ABD和△ADC中,底BD=DC,高相等,
∴S△ABD=S△ADC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×8=4cm2,
在△AEF和△DEF中,底AF=3FD,高相等,
∴S△AEF=3S△DEF,
设S△DEF=tcm2,则S△AEF=3tcm2,
S△DCE=S△ACD-S△AEF-S△DEF=4-4tcm2,
在△ABF和△BDF中,底AF=3FD,高相等,
∴3S△BDF=S△ABF,
∵S△ABD=4cm2,S△ABD=S△ABF+S△BDF,
∴S△BDF=1cm2,
在△BDE和△DCE中,底BD=DC,高相等,
∴S△BDE=S△DCE,即1+t=4-4t,
解得t=0.6cm2.
故答案为:4;0.6.
点评 本题考查了三角形的面积,解题的关键是:在高相等的情况下,面积比等于底边比.

练习册系列答案
相关题目
2.已知:有理数满足(m+$\frac{n}{4}$)2+|n2-4|=0,则m2n2的值为( )
| A. | ±1 | B. | 1 | C. | ±2 | D. | 2 |
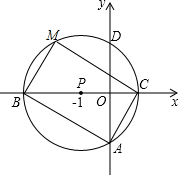 如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2$\sqrt{3}$,将△ABC绕点P旋转180°,得到△MCB.
如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2$\sqrt{3}$,将△ABC绕点P旋转180°,得到△MCB. 某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)
某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,$\sqrt{3}$≈1.7)