题目内容
10.抛物线y=ax2+bx+c(a>0)的对称轴为x=1,它与x轴的一个交点的坐标为(-3,0),则它与x轴另一个交点的坐标为( )| A. | (-2,0) | B. | (-1,0) | C. | (2,0) | D. | (5,0) |
分析 根据抛物线的对称性和对称轴为x=1,它与x轴的一个交点的坐标为(-3,0),即可求出另一个交点坐标.
解答 解:∵抛物线y=ax2+bx+c(a>0)的对称轴为x=1,它与x轴的一个交点的坐标为(-3,0),
则设抛物线与x轴的另一个交点坐标为(m,0),
根据题意得$\frac{m-3}{2}=1$,
解得m=5,
∴抛物线与x轴的另一个交点坐标为(5,0).
故选D.
点评 本题主要考查了抛物线与x轴的交点,利用抛物线的对称性是解答此题的关键.

练习册系列答案
相关题目
19.把12+(+9)+(-6)写成省略加号的和的形式,正确的是( )
| A. | 12-9-6 | B. | 12+9-6 | C. | -12+9+6 | D. | 12-9+6 |
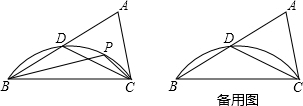
 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).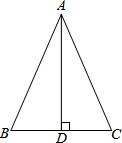 如图,等腰△ABC中,AB=AC=13cm,BC=10cm,求外接圆的半径.
如图,等腰△ABC中,AB=AC=13cm,BC=10cm,求外接圆的半径.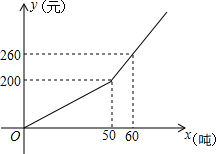 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.