题目内容
5. 如图,等腰△ABC中,AB=AC=13cm,BC=10cm,求外接圆的半径.
如图,等腰△ABC中,AB=AC=13cm,BC=10cm,求外接圆的半径.
分析 设O为△ABC外接圆的圆心,连接AO,且延长AO交BC于D,连接OB、OC,求出AD⊥BC,BD=DC,根据勾股定理求出AD,设等腰△ABC外接圆的半径,在Rt△OBD中,由勾股定理得出OB2=OD2+BD2,代入求出即可.
解答 解:设O为△ABC外接圆的圆心,连接AO,且延长AO交BC于D,连接OB、OC,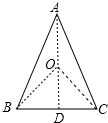
∵AB=AC,O为△ABC外接圆的圆心,
∴AD⊥BC,BD=DC,
BD=DC=$\frac{1}{2}$BC=5,
设等腰△ABC外接圆的半径为R,
则OA=OB=OC=R,
在Rt△ABD中,由勾股定理得:AD=12,
在Rt△OBD中,由勾股定理得:OB2=OD2+BD2,
即R2=(12-R)2+52,
R=$\frac{169}{24}$.
答:等腰△ABC外接圆的半径为$\frac{169}{24}$.
点评 本题考查了三角形的外接圆、勾股定理、等腰三角形的性质、方程的应用,掌握外心的性质、根据勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
8.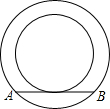 如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
 如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
10.抛物线y=ax2+bx+c(a>0)的对称轴为x=1,它与x轴的一个交点的坐标为(-3,0),则它与x轴另一个交点的坐标为( )
| A. | (-2,0) | B. | (-1,0) | C. | (2,0) | D. | (5,0) |
15.一个直角三角形的两条直角边相差5cm,面积是7cm2,斜边长是( )
| A. | $\sqrt{14}$ | B. | $\sqrt{35}$ | C. | $\sqrt{53}$ | D. | $\sqrt{74}$ |
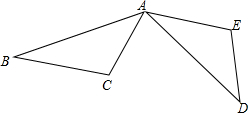 如图,△ABC按逆时针方向旋转得到△ADE
如图,△ABC按逆时针方向旋转得到△ADE