题目内容
20．
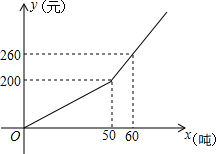已知某市2013年企业用水量x（吨）与该月应交的水费y（元）之间的函数关系如图．（1）当x≥50时，求y关于x的函数关系式；
（2）为贯彻省委“五水共治”发展战略，鼓励企业节约用水，该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费，规定：若企业月用水量x超过80吨，则除按2013年收费标准收取水费外，超过80吨部分每吨另加收$\frac{x}{20}$元，若某企业2014年3月份的水费和污水处理费共600元，求这个企业该月的用水量．
分析 （1）设y关于x的函数关系式y=kx+b，代入（50，200）、（60，260）两点求得解析式即可；
（2）利用水费+污水处理费=600元，列出方程解决问题．
解答 解：（1）设y关于x的函数关系式y=kx+b，
∵直线y=kx+b经过点（50，200），（60，260）
∴$\left\{\begin{array}{l}{50k+b=200}\\{60k+b=260}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=6}\\{b=-100}\end{array}\right.$．
∴y关于x的函数关系式是y=6x-100；
（2）由题意得6x-100+$\frac{x}{20}$（x-80）=600，
化简得x2+40x-14000=0，
解得：x1=100，x2=-140（不合题意，舍去）．
答：这个企业2014年3月份的用水量是100吨．
点评 此题考查一次函数的运用，一元二次方程和一元一次方程的运用，注意理解题意，结合图象，根据实际选择合理的方法解答．
练习册系列答案
相关题目
10．抛物线y=ax2+bx+c（a＞0）的对称轴为x=1，它与x轴的一个交点的坐标为（-3，0），则它与x轴另一个交点的坐标为（ ）
| A． | （-2，0） | B． | （-1，0） | C． | （2，0） | D． | （5，0） |
11．在“母亲节”期间，某校部分团员参加社会公益活动，准备构建一批许愿瓶进行销售，并将所得利润捐给慈善机构，根据市场调查，这种许愿瓶一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如表所示：
（1）试判断y与x之间的函数关系，并求出函数关系式；
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（元）与销售单价x（元/个）之间的函数关系式；为了方便顾客，售价定位多少时可获利1200元；
（3）若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定此时的销售单价，并求出此时的最大利润．
（1）试判断y与x之间的函数关系，并求出函数关系式；
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（元）与销售单价x（元/个）之间的函数关系式；为了方便顾客，售价定位多少时可获利1200元；
（3）若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定此时的销售单价，并求出此时的最大利润．
| z（元/个） | 16 | 14 | 12 | 10 |
| y（个） | 120 | 180 | 240 | 300 |
15．一个直角三角形的两条直角边相差5cm，面积是7cm2，斜边长是（ ）
| A． | $\sqrt{14}$ | B． | $\sqrt{35}$ | C． | $\sqrt{53}$ | D． | $\sqrt{74}$ |
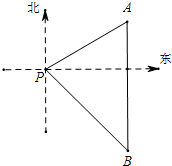一艘海轮位于灯塔P的北偏东60°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的东南方向上的B处．这时，海轮所在的B处距离灯塔P有多远？（结果保留根号）
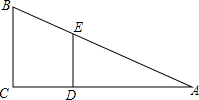如图，上体育课，九年级三班的甲、乙两名同学分别站在C、D的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距1米．甲身高1.8米，乙身高1.5米，则甲的影长是（ ）