题目内容
5. 如图,矩形ABCD∽矩形ECDF,且AB=BE,求BC与AB的比值.
如图,矩形ABCD∽矩形ECDF,且AB=BE,求BC与AB的比值.
分析 根据相似多边形的性质列出比例式,得到一元二次方程,解方程即可.
解答 解:∵矩形ABCD∽矩形ECDF,
∴$\frac{BC}{CD}$=$\frac{CD}{EC}$,即$\frac{BC}{CD}$=$\frac{CD}{BC-AB}$,
∴BC2-BC•AB-CD2=0,
解得,BC=$\frac{1±\sqrt{5}}{2}$CD,
∵BC、CD是正数,
∴$\frac{BC}{AB}$=$\frac{1+\sqrt{5}}{2}$.
点评 本题考查的是相似多边形的性质,掌握相似多边形的对应边的比相等是解题的关键.

练习册系列答案
相关题目
10.下列方程中,解为x=1的是( )
| A. | x-2=-1 | B. | 2x+3=1 | C. | 1=1+x | D. | 2x-3=1 |
14.若直角三角形的三边长为偶数,则这三边的边长可能是( )
| A. | 3,4,5 | B. | 6,8,10 | C. | 7,24,29 | D. | 8,12,20 |
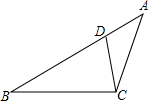 已知:如图,在△ABC中,D是AB上一点,且∠ACD=∠B,若AC=5,AB=9,CB=6.
已知:如图,在△ABC中,D是AB上一点,且∠ACD=∠B,若AC=5,AB=9,CB=6. 如图,五边形ABCDE与五边形A′B′C′D′E′位似,对应边CD=2,C′D′=3,则AB:A′B′=2:3.
如图,五边形ABCDE与五边形A′B′C′D′E′位似,对应边CD=2,C′D′=3,则AB:A′B′=2:3.