题目内容
8. 如图,在梯形ABCD中,AD∥BC,EF∥BC,EF分别交AB,CD,AC于点E、F、G.若$\frac{CF}{FD}$=$\frac{2}{3}$,则$\frac{BE}{EA}$=$\frac{2}{3}$,$\frac{CG}{CA}$=$\frac{2}{5}$,$\frac{AG}{AC}$=$\frac{3}{5}$,$\frac{AB}{EB}$=$\frac{5}{2}$.
如图,在梯形ABCD中,AD∥BC,EF∥BC,EF分别交AB,CD,AC于点E、F、G.若$\frac{CF}{FD}$=$\frac{2}{3}$,则$\frac{BE}{EA}$=$\frac{2}{3}$,$\frac{CG}{CA}$=$\frac{2}{5}$,$\frac{AG}{AC}$=$\frac{3}{5}$,$\frac{AB}{EB}$=$\frac{5}{2}$.
分析 由$\frac{CF}{FD}$=$\frac{2}{3}$,平行线分线段成比例直接得出$\frac{BE}{EA}$=$\frac{2}{3}$,进一步利用份数和对应线段成比例得出答案即可.
解答 解:∵AD∥BC,EF∥BC,$\frac{CF}{FD}$=$\frac{2}{3}$,
∴$\frac{BE}{EA}$=$\frac{2}{3}$,$\frac{CG}{CA}$=$\frac{2}{2+3}$=$\frac{2}{5}$,$\frac{AG}{AC}$=$\frac{3}{2+3}$=$\frac{3}{5}$,$\frac{AB}{EB}$=$\frac{2+3}{2}$=$\frac{5}{2}$.
故答案为:$\frac{2}{3}$,$\frac{2}{5}$,$\frac{3}{5}$,$\frac{5}{2}$.
点评 此题考查了平行线分线段成比例定理,注意线段的对应,利用份数解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.AB、CD是半径为5的⊙O的两条弦,若AB∥CD,AB=8,CD=6,则平行直线AB、CD的距离是( )
| A. | 1 | B. | 5 | C. | 7 | D. | 1或7 |
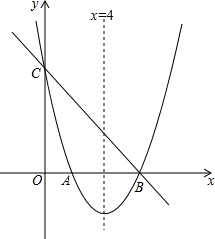 如图所示,抛物线y=ax2+bx+c与直线y=-x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4.
如图所示,抛物线y=ax2+bx+c与直线y=-x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4. 在矩形ABCD中,AB=12,AD=5,以点A为圆心,r为半径作圆.
在矩形ABCD中,AB=12,AD=5,以点A为圆心,r为半径作圆.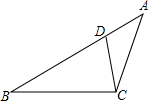 已知:如图,在△ABC中,D是AB上一点,且∠ACD=∠B,若AC=5,AB=9,CB=6.
已知:如图,在△ABC中,D是AB上一点,且∠ACD=∠B,若AC=5,AB=9,CB=6. 如图,五边形ABCDE与五边形A′B′C′D′E′位似,对应边CD=2,C′D′=3,则AB:A′B′=2:3.
如图,五边形ABCDE与五边形A′B′C′D′E′位似,对应边CD=2,C′D′=3,则AB:A′B′=2:3.