题目内容
13.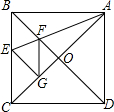 如图,在正方形ABCD中,对角线AC、BD相交于点O,E是BC边上一点,连结AE交BD于点F,G是AC上一点,B、G关于直线AE对称.求证:四边形BEGF为菱形,并请直接写出图中与线段AG相等的所有线段.
如图,在正方形ABCD中,对角线AC、BD相交于点O,E是BC边上一点,连结AE交BD于点F,G是AC上一点,B、G关于直线AE对称.求证:四边形BEGF为菱形,并请直接写出图中与线段AG相等的所有线段.
分析 首先根据轴对称的性质可得AE垂直平分BG,进而利用垂直平分线的性质得到AB=AG,BF=GF,BE=EG,然后结合正方形的性质可以求出∠1,∠2,∠BEA,∠BFE的度数,进而得到∠BEA=∠BFE,并利用等角对等边可知BE=BF,从而得到BE=EG=BF=GF,利用菱形的判定方法可知四边形BEGF是菱形,再结合正方形的性质可知正方形的各边与AG相等,可求得∠AFD=∠FAD=67.5°,进而可知DF=AD,即可得出与AG相等的线段.
解答 证明:在正方形ABCD中,∠CBA=90°,∠CAB=45°,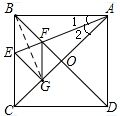
连结BG,
∵B、G关于直线AE对称,
∴AE垂直平分BG,
∴AB=AG,BF=GF,BE=EG,
∵AE⊥BG,
∴∠1=∠2=$\frac{1}{2}∠BAC$=22.5°,
∴∠BEA=90°-∠1=67.5°,
∴∠BFE=∠1+∠DBA=67.5°,
∴∠BEA=∠BFE,
∴BE=BF,
∴BE=EG=BF=GF,
∴四边形BEGF为菱形,
与AG相等的线段有AB、BC、CD、AD、DF.
点评 本题综合考查了菱形的判定,轴对称的性质,垂直平分线的性质,正方形的性质,等腰三角形的判定等知识,具有一定的综合性,正确识图并熟知各个性质与判定是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
5.直线y=kx-4经过点(-2,2),则该直线的解析式是( )
| A. | y=x-4 | B. | y=-x-4 | C. | y=-3x-4 | D. | y=3x-4 |
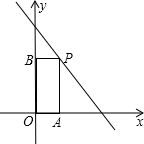 如图,在一次函数y=-x+10的图象上取一点P,作PA⊥x轴,PB⊥y轴,垂足为B,且矩形PBOA的面积为9,则这样的点P个数共有( )
如图,在一次函数y=-x+10的图象上取一点P,作PA⊥x轴,PB⊥y轴,垂足为B,且矩形PBOA的面积为9,则这样的点P个数共有( ) 如图,是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的小立方块的个数,这个几何体的左视图是( )
如图,是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的小立方块的个数,这个几何体的左视图是( )



 如图是某工件的三视图,求此工件的全面积和体积.
如图是某工件的三视图,求此工件的全面积和体积. 如图是由若干个边长为a的大小相同的小正方体组成的几何体,这个几何体的表面积是28a2.(用a的代数式表示)
如图是由若干个边长为a的大小相同的小正方体组成的几何体,这个几何体的表面积是28a2.(用a的代数式表示)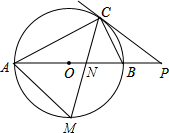 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠ACB的平分线CM分别与AB,⊙O交于点N,M,且PC=PN.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠ACB的平分线CM分别与AB,⊙O交于点N,M,且PC=PN.