题目内容
8.在下列命题中:①平分弦的直径垂直于弦;②斜边长为6的直角三角形的重心到其外心的距离为1;③线段AB上一点C满足AC=$\frac{3-\sqrt{5}}{2}$AB,则点C为线段AB的黄金分割点;④所有角都对应相等的两个多边形相似;⑤相等的弦所对的弧相等;⑥圆内接四边形对角互补.其中真命题的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据垂径定理对①进行判断;根据直角三角形的外心为斜边的中点和重心的定义对②进行判断;根据黄金分割的定义对③进行判断;根据多边形相似的判定对④进行判断;根据圆心角、弧、弦的关系对⑤进行判断;根据圆内接四边形的性质对⑥进行判断.
解答 解:平分弦(非直径)的直径垂直于弦,所以①错误;斜边长为6的直角三角形的重心到其外心的距离为1,所以②正确;线段AB上一点C满足AC=$\frac{3-\sqrt{5}}{2}$AB,则BC=$\frac{\sqrt{5}-1}{2}$AB,所以点C为线段AB的黄金分割点,所以③正确;所有角都对应相等,对应边的比相等的两个多边形相似,所以④正确;在同圆或等圆中,相等的弦所对的弧对应相等,所以⑤错误;圆内接四边形对角互补,所以⑥正确.
故选B.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.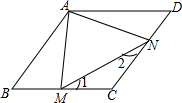 在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )
在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )
 在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )
在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )| A. | 120° | B. | 100° | C. | 80° | D. | 60° |
8.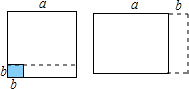 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | (a-b)2=a2-2ab-b2. |
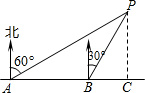 如图,小明同学在东西走向的山阴路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东200米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到山阴路的距离PC为100$\sqrt{3}$米.
如图,小明同学在东西走向的山阴路A处,测得一处公共自行车租用服务点P在北偏东60°方向上,在A处往东200米的B处,又测得该服务点P在北偏东30°方向上,则该服务点P到山阴路的距离PC为100$\sqrt{3}$米.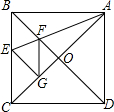 如图,在正方形ABCD中,对角线AC、BD相交于点O,E是BC边上一点,连结AE交BD于点F,G是AC上一点,B、G关于直线AE对称.求证:四边形BEGF为菱形,并请直接写出图中与线段AG相等的所有线段.
如图,在正方形ABCD中,对角线AC、BD相交于点O,E是BC边上一点,连结AE交BD于点F,G是AC上一点,B、G关于直线AE对称.求证:四边形BEGF为菱形,并请直接写出图中与线段AG相等的所有线段.