题目内容
12.已知抛物线y=ax2+bx+c(a≠0)过点(2,0)和点(1,-3),且顶点在第三象限,点P(-1,m)在该抛物线上,则m的取值范围是( )| A. | -6<m<-4 | B. | -9<m<-3 | C. | m>-9 | D. | m<-4 |
分析 根据题意得出$\left\{\begin{array}{l}{4a+2b+c=0①}\\{a+b+c=-3②}\\{a-b+c=m③}\end{array}\right.$,②-③得,2b=-m-3,得出b=-$\frac{m+3}{2}$,①-②得,3a+b=3.得出a=1-$\frac{1}{3}$b=1+$\frac{m+3}{6}$=$\frac{m+9}{6}$,根据顶点在第三象限,得出-$\frac{b}{2a}$=-$\frac{-\frac{m+3}{2}}{2×\frac{m+9}{6}}$=$\frac{3(m+3)}{2(m+9)}$<0,即可求得-9<m<-3.
解答 解:∵点(2,0)、点(1,-3)、点P(-1,m)在抛物线上,
∴$\left\{\begin{array}{l}{4a+2b+c=0①}\\{a+b+c=-3②}\\{a-b+c=m③}\end{array}\right.$
②-③得,2b=-m-3,
∴b=-$\frac{m+3}{2}$,
①-②得,3a+b=3.
∴a=1-$\frac{1}{3}$b=1+$\frac{m+3}{6}$=$\frac{m+9}{6}$,
∵-$\frac{b}{2a}$=-$\frac{-\frac{m+3}{2}}{2×\frac{m+9}{6}}$=$\frac{3(m+3)}{2(m+9)}$,
∵顶点在第三象限,
∴$\frac{3(m+3)}{2(m+9)}$<0,
∴$\left\{\begin{array}{l}{m+3>0}\\{m+9<0}\end{array}\right.$或$\left\{\begin{array}{l}{m+3<0}\\{m+9>0}\end{array}\right.$,
解得-9<m<-3,
故选B.
点评 本题考查了二次函数图象上点的坐标特征,以及二次函数的性质;二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c).

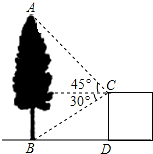 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)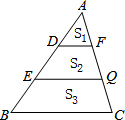 如图,在△ABC中,DF∥EQ∥BC,且AD=DE=EB,△ABC被DF、EQ分成三部分,且三部分面积分别为S1,S2,S3,则S1:S2:S3=1:3:5.
如图,在△ABC中,DF∥EQ∥BC,且AD=DE=EB,△ABC被DF、EQ分成三部分,且三部分面积分别为S1,S2,S3,则S1:S2:S3=1:3:5.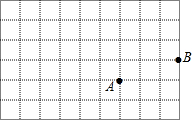 在正方形的网格中,每个小正方形的边长都为1,格点A、B的位置如图所示:
在正方形的网格中,每个小正方形的边长都为1,格点A、B的位置如图所示: