题目内容

20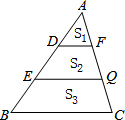．如图，在△ABC中，DF∥EQ∥BC，且AD=DE=EB，△ABC被DF、EQ分成三部分，且三部分面积分别为S1，S2，S3，则S1：S2：S3=1：3：5．

分析 根据DF∥EQ∥BC，判断出△ADF∽△AEG∽△ABC，再根据相似三角形的面积比等于相似比的平方解答即可．

解答 解：∵DF∥EG∥BC，
∴△ADF∽△AEG∽△ABC，
又∵AD=DE=EB，
∴三个三角形的相似比是1：2：3，
∴面积的比是1：4：9，
设△ADF的面积是a，则△AEG与△ABC的面积分别是4a，9a，
∴S2=3a，S3=5a，则Sl：S2：S3=1：3：5．
故答案为：1：3：5．

点评 本题考查了相似三角形的判定和性质，熟练掌握相似三角形的面积的比等于相似比的平方是解题的关键．

练习册系列答案
相关题目
10．下列图案中，既是轴对称图形，又是中心对称图形的是（　　）
A．B．C．D．
11．已知直角三角形斜边长为（2$\sqrt{6}$+$\sqrt{3}$）cm，一直角边长为（$\sqrt{6}$+2$\sqrt{3}$）cm，求这个直角三角形的面积．
8．用6个小正方体搭成的几何体如图，请画出它的三视图．
 
15．设a、b是两个整数，若定义一种运算“△”，a△b=a2+ab，则方程x△（x-2）=12的实数根是（　　）
A．x1=-2，x2=3B．x1=2，x2=-3C．x1=-1，x2=6D．x1=1，x2=-6
5．若把分式$\frac{x+y}{2xy}$中的x和y都扩大3倍，那么分式的值为原来的（　　）
A．3倍B．不变C．$\frac{1}{3}$D．6倍
12．已知抛物线y=ax2+bx+c（a≠0）过点（2，0）和点（1，-3），且顶点在第三象限，点P（-1，m）在该抛物线上，则m的取值范围是（　　）
A．-6＜m＜-4B．-9＜m＜-3C．m＞-9D．m＜-4
9．如图，四边形OABC为菱形，点B、C在以点O为圆心的$\widehat{EF}$上，若OA=1cm，∠1=∠2，则$\widehat{EF}$的长为$\frac{2π}{3}$cm．
10．已知一次函数y=kx+b的图象经过第一、二、三象限，则b的值可以是（　　）
A．2B．0C．-1D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网