题目内容
4.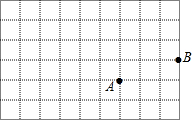 在正方形的网格中,每个小正方形的边长都为1,格点A、B的位置如图所示:
在正方形的网格中,每个小正方形的边长都为1,格点A、B的位置如图所示:(1)画出适当的平面直角坐标系,使点A、B的坐标分别为(1,2)、(4,3).
(2)在(1)中画出的坐标系中标出点C(3,6),并连接AB、AC、BC.则△ABC 的面积=5.
(3)画出△ABC关于y轴的对称图形△A′B′C′.
分析 (1)根据A、B两点的坐标建立直角坐标系即可;
(2)在坐标系内找出点C,连接AB、AC、BC,利用矩形的面积减去三角形三个顶点上三角形的面积即可;
(3)作出各点关于y轴的对称点,再顺次连接即可.
解答 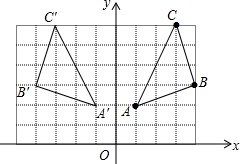 解:(1)如图所示;
解:(1)如图所示;
(2)S△ABC=3×4-$\frac{1}{2}$×3×1-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×
4
=12-$\frac{3}{2}$-$\frac{3}{2}$-4
=5.
故答案为:5;
(3)如图所示,△A′B′C′即为所求.
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设a、b是两个整数,若定义一种运算“△”,a△b=a2+ab,则方程x△(x-2)=12的实数根是( )
| A. | x1=-2,x2=3 | B. | x1=2,x2=-3 | C. | x1=-1,x2=6 | D. | x1=1,x2=-6 |
12.已知抛物线y=ax2+bx+c(a≠0)过点(2,0)和点(1,-3),且顶点在第三象限,点P(-1,m)在该抛物线上,则m的取值范围是( )
| A. | -6<m<-4 | B. | -9<m<-3 | C. | m>-9 | D. | m<-4 |
16.一次函数y=-2x+1的图象与y轴的交点坐标是( )
| A. | (-2,0) | B. | ($\frac{1}{2}$,0) | C. | (0,2) | D. | (0,1) |
14.某圆锥的母线长为6cm,其底面圆半径为3cm,则它的侧面积为( )
| A. | 18πcm2 | B. | 18cm2 | C. | 36πcm2 | D. | 36cm2 |
 如图,四边形OABC为菱形,点B、C在以点O为圆心的$\widehat{EF}$上,若OA=1cm,∠1=∠2,则$\widehat{EF}$的长为$\frac{2π}{3}$cm.
如图,四边形OABC为菱形,点B、C在以点O为圆心的$\widehat{EF}$上,若OA=1cm,∠1=∠2,则$\widehat{EF}$的长为$\frac{2π}{3}$cm.