题目内容
2.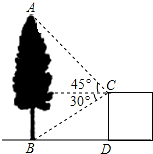 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)
分析 作CE⊥AB于点E,则△BCE和△BCD都是直角三角形,即可求得CE,BE的长,然后在Rt△ACE中利用三角函数求得AE的长,进而求得AB的长,即为大树的高度.
解答 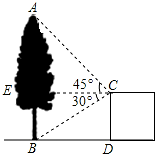 解:作CE⊥AB于点E,
解:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=6m,
CE=$\frac{BE}{tan30°}$=6$\sqrt{3}$m,
在Rt△ACE中,
AE=CE•tan45°=6$\sqrt{3}$m,
AB=BE+AE=(6+$\sqrt{3}$6)m.
答:大树的高度为(6+6$\sqrt{3}$)m.
点评 本题考查解直角三角形的应用-仰角俯角问题的应用,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
10.下列图案中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.已知抛物线y=ax2+bx+c(a≠0)过点(2,0)和点(1,-3),且顶点在第三象限,点P(-1,m)在该抛物线上,则m的取值范围是( )
| A. | -6<m<-4 | B. | -9<m<-3 | C. | m>-9 | D. | m<-4 |
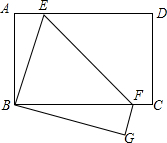 已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF,射线ED分别交于点M、N,当EN=MN时,则FM的长为$\frac{5}{4}$.
已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF,射线ED分别交于点M、N,当EN=MN时,则FM的长为$\frac{5}{4}$. 已知:数a,b,c 在数轴上的对应点如右图所示,
已知:数a,b,c 在数轴上的对应点如右图所示,