题目内容
17．用等式性质解释，能否从等式（3a+7）x=4a-b中得到x=$\frac{4a-b}{3a+7}$？反过来，能否从等式x=$\frac{4a-b}{3a+7}$中得到（3a+7）x=4a-b？分析 利用等式的性质2进行判断即可．
解答 解：当3a+7=0时，不能得到x=$\frac{4a-b}{3a+7}$，当3a+7≠0时，能得到x=$\frac{4a-b}{3a+7}$，故从等式（3a+7）x=4a-b中不一定能得到x=$\frac{4a-b}{3a+7}$；
由等式的性质2两边同时乘以3a+7可知：（3a+7）x=4a-b，故从等式x=$\frac{4a-b}{3a+7}$能得到（3a+7）x=4a-b．
点评 本题主要考查的是等式的性质，明确利用等式性质2对等式进行变形时，除数不能为0是解题的关键．
练习册系列答案
三点一测快乐周计划系列答案
相关题目
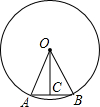如图，⊙O的半径为20，$\widehat{AB}$的度数为36°，求弦AB及其弦心距OC的长（精确到0.1）．
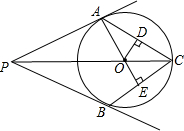从⊙O外一点P引⊙O的切线PA、PB，切点分别为A、B两点，连结PO并延长PO交⊙O于点C，连接CA，CB，OD⊥AC，OE⊥CB，垂足分别为D、E，求证：OD=OE．