题目内容
7.某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查,下面是根据收集的数据绘制的两幅不完整的统计图.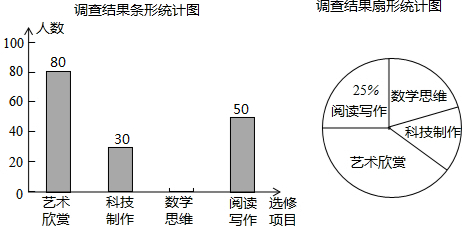
根据图中提供的信息,解答下列问题:
(1)此次共调查了200名学生,扇形统计图中,“艺术鉴赏”所对应的圆心角的度数是144度;
(2)请把这个条形统计图补充完整;
(3)现该校700名学生报名参加这四个选修项目,请你估计有多少名学生参加了“数学思维”项目.
分析 (1)根据总人数=所占人数÷百分数,圆心角=360°×百分比,分别计算即可;
(2)求出数学思维的人数,画出条形图即可;
(3)用样本估计总体的思想思考问题即可;
解答 解:(1)总人数=50÷25%=200人,
艺术鉴赏”所对应的圆心角的度数=360°×$\frac{80}{200}$=144°,
故答案为200,144.
(2)数学思维的人数=200-80-30-50=40(人),
条形图如图所示,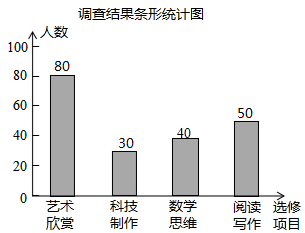
(3)该校700名学生有700×$\frac{40}{200}$=140名学生参加了“数学思维”项目.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图中各部分占总体的百分比之和为1,直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
18.甲、乙两同学的五次数学测验成绩如下:
如果这个班数学成绩的平均数为75分,试根据以上数据,对甲、乙两名学生的数学学习状况作出分析.
| 甲 | 81 | 98 | 76 | 95 | 100 |
| 乙 | 86 | 88 | 91 | 93 | 92 |
15.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用-支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
| x(人) | 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
| y(元) | -3000 | -2000 | -1000 | 0 | 1000 | 2000 | … |
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
19.下列各式的计算中,正确的是( )
| A. | $\sqrt{(-16)×(-25)}$=$\sqrt{(-16)}$×$\sqrt{(-25)}$=20 | B. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | ||
| C. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{81×1}$=9 | D. | 3$\sqrt{\frac{2}{3}}$=$\sqrt{2}$ |
16.下列方程中,无理方程是( )
| A. | $\sqrt{2}$x2-1=0 | B. | 1-$\frac{\sqrt{2}}{x}$=0 | C. | $\sqrt{2x}$-1=0 | D. | 1-$\sqrt{2}x$=0 |
17.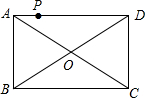 如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
 如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )| A. | 4.8 | B. | 5 | C. | 6 | D. | 7.2 |