题目内容
17.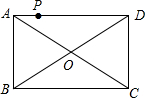 如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一动点,AB=6,BC=8,则点P到矩形的两条对角线AC和BD的距离之和是( )| A. | 4.8 | B. | 5 | C. | 6 | D. | 7.2 |
分析 过P作PE⊥AC于点E,作PF⊥BD于点F,过O作OG⊥AD,连接OP,利用等积法可求得答案.
解答  解:
解:
如图,过P作PE⊥AC于点E,作PF⊥BD于点F,过O作OG⊥AD,连接OP,
∵四边形ABCD为矩形,
∴∠ABC=90°,
∵AB=6,BC=8,
∴AC=BD=10,
∴AO=OD=5,GO=$\frac{1}{2}$AB=3,
∵S△AOD=S△AOP+S△DOP,
∴$\frac{1}{2}$AD•GO=$\frac{1}{2}$AO•PE+$\frac{1}{2}$DO•PF,
∴8×3=5PE+5PF,
∴PE+PF=$\frac{24}{5}$=4.8,
即点P到到矩形的两条对角线AC和BD的距离之和是4.8,
故选A.
点评 本题主要考查矩形的性质,掌握矩形的对角线相等且平分是解题的关键,注意等积法的应用.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
12.下列二次根式能与$\sqrt{6}$合并的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{24}$ | D. | $\sqrt{30}$ |
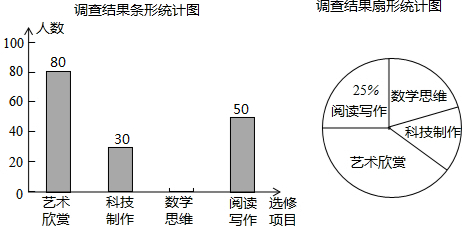
7.对于条形统计图、折线统计图和扇形统计图这三种常见的统计图,下列说法正确的是( )
| A. | 通常不可互相转换 | |
| B. | 扇形统计图能清楚地表示出各部分在总体中所占的百分比 | |
| C. | 折线统计图能清楚地表示出每个项目的具体数目 | |
| D. | 条形统计图能清楚地反映事物的变化情况 |
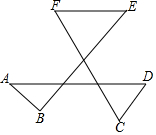 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是360°.
如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是360°. 如图,已知:AC∥FG,∠1=∠2,判断DE与FG的位置关系,并说明理由.
如图,已知:AC∥FG,∠1=∠2,判断DE与FG的位置关系,并说明理由. 如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为24,则BC的长为( )
如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为24,则BC的长为( )