题目内容
抛物线y=-x2+2x+c与x轴交于A(-1,0),该抛物线顶点坐标 .
考点:二次函数的性质
专题:计算题
分析:先把A点坐标代入y=-x2+2x+c求出c得到抛物线解析式,然后把解析式配成顶点式,再利用二次函数的性质确定顶点坐标.
解答:解:把A(-1,0)代入y=-x2+2x+c得-1-2+c=0,解得c=3,
所以y=-x2+2x+3=-(x-1)2+4,
所以抛物线得顶点坐标为(1,4).
故答案为(1,4).
所以y=-x2+2x+3=-(x-1)2+4,
所以抛物线得顶点坐标为(1,4).
故答案为(1,4).
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
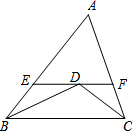 已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F.AB=8,AC=6,求三角形AEF的周长.
已知:△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F.AB=8,AC=6,求三角形AEF的周长.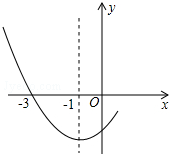 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④m(am+b)≥a-b(m为任意实数);⑤若(-5,y1),(2,y2)是抛物线上两点,则y1>y2.其中说法正确的个数是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④m(am+b)≥a-b(m为任意实数);⑤若(-5,y1),(2,y2)是抛物线上两点,则y1>y2.其中说法正确的个数是( ) 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.