题目内容
已知抛物线y=-x2与直线y=2x-3相交于点A(1,a),求:
(1)a的值;
(2)另一个交点B的坐标;
(3)△AOB的面积.
(1)a的值;
(2)另一个交点B的坐标;
(3)△AOB的面积.
考点:二次函数的性质
专题:计算题
分析:(1)直接把A(1,a)代入直线y=2x-3可求出a的值;
(2)根据二次函数图象与一次函数图象的交点问题,解方程组
即可得到另一个交点B的坐标;
(3)先确定直线y=2x-3与y轴交于点C的坐标,然后根据三角形面积公式和△AOB的面积=S△OAC+S△OBC进行计算.
(2)根据二次函数图象与一次函数图象的交点问题,解方程组
|
(3)先确定直线y=2x-3与y轴交于点C的坐标,然后根据三角形面积公式和△AOB的面积=S△OAC+S△OBC进行计算.
解答:解:(1)把A(1,a)代入y=2x-3得2-3=a,
所以a=-1;
(2)解方程组
得
或
,
所以另一个交点B的坐标为(-3,-9);
(3)如图,直线y=2x-3与y轴交于点C(0,-3),
所以△AOB的面积=S△OAC+S△OBC
=
•3•1+
•3•3
=6.

所以a=-1;
(2)解方程组
|
|
|
所以另一个交点B的坐标为(-3,-9);
(3)如图,直线y=2x-3与y轴交于点C(0,-3),
所以△AOB的面积=S△OAC+S△OBC
=
| 1 |
| 2 |
| 1 |
| 2 |
=6.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
.也考查了二次函数图象与一次函数图象的交点问题.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |

练习册系列答案
相关题目
下列结论正确的是( )
| A、a一定是正数 |
| B、倒数等于它本身的数只有1 |
| C、面积为2的正方形的边长a是无理数 |
| D、0是最小的整数 |
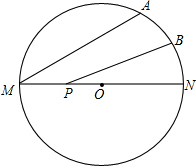 如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
如图,MN是半径为2的⊙O的直径,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )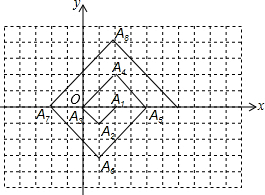 如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的坐标为
如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的坐标为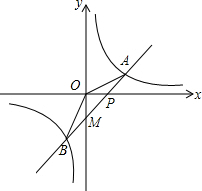 如图,一次函数y=kx-1的图象和反比例函数y=
如图,一次函数y=kx-1的图象和反比例函数y=