题目内容
计算:
+(
+
)+(
+
+
)+…+(
+
+…
)
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 6 |
| 3 |
| 6 |
| 5 |
| 6 |
| 1 |
| 98 |
| 3 |
| 98 |
| 97 |
| 98 |
考点:有理数的加法
专题:计算题
分析:原式括号中利用同分母分数的加法法则计算,利用连续奇数之和等于个数的平方即1+3+5+…+2n-1=n2,计算变形,计算即可得到结果.
解答:解:原式=
+
+
+…+
=
+
+
+…+
=
+
+
+…+
=
(1+2+…+49)
=
=612.5.
| 1 |
| 2 |
| 1+3 |
| 4 |
| 1+3+5 |
| 6 |
| 1+3+5+…+97 |
| 98 |
=
| 12 |
| 2×1 |
| 22 |
| 2×2 |
| 32 |
| 2×3 |
| 492 |
| 2×49 |
=
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 49 |
| 2 |
=
| 1 |
| 2 |
=
| 49×(1+49) |
| 4 |
=612.5.
点评:此题考查了有理数的加法,熟练掌握加法法则是解本题的关键.

练习册系列答案
相关题目
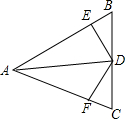 如图,AD平分线∠BAC,AE=AF,则下列说法:①△EAD≌△FAD;②∠AED=∠AFD;③BD=CD;④AD⊥BC.其中正确的有( )
如图,AD平分线∠BAC,AE=AF,则下列说法:①△EAD≌△FAD;②∠AED=∠AFD;③BD=CD;④AD⊥BC.其中正确的有( )
