题目内容
如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1=∠C．（1）求证：CB∥PD；
（2）若AB=5，sin∠P=
| 3 |
| 5 |
考点：圆周角定理,垂径定理
专题：证明题
分析：（1）根据圆周角定理得∠C=∠P，加上∠1=∠C，则∠1=∠P，然后根据平行线的判定方法即可得到CB∥PD；
（2）连结AC，如图，根据垂径定理，由CD⊥AB得到
=
，再根据圆周角定理得∠A=∠P，接着由AB为直径得到∠ACB=90°，然后在Rt△ACB中，利用∠A的正弦求BC的长．
（2）连结AC，如图，根据垂径定理，由CD⊥AB得到
 |
| BC |
|
| BD |
解答：（1）证明：∵∠C=∠P，
而∠1=∠C，
∴∠1=∠P，
∴CB∥PD；
（2）解：连结AC，如图，
∵CD⊥AB，
∴
=
，
∴∠A=∠P，
∴sinA=sin∠P=
，
∵AB为直径，
∴∠ACB=90°，
在Rt△ACB中，
sinA=
=
，
而AB=5，
∴BC=3．
而∠1=∠C，
∴∠1=∠P，
∴CB∥PD；
（2）解：连结AC，如图，
∵CD⊥AB，
∴
|
| BC |
|
| BD |
∴∠A=∠P，
∴sinA=sin∠P=
| 3 |
| 5 |
∵AB为直径，
∴∠ACB=90°，
在Rt△ACB中，
sinA=
| BC |
| AB |
| 3 |
| 5 |
而AB=5，
∴BC=3．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了垂径定理和锐角三角函数．
练习册系列答案
相关题目
下列结论正确的是（ ）
| A、a一定是正数 |
| B、倒数等于它本身的数只有1 |
| C、面积为2的正方形的边长a是无理数 |
| D、0是最小的整数 |
如图，数轴上与1、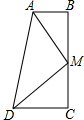
已知，如图∠B=∠C=90°，M是BC的中点，DM平分∠ADC．