题目内容
19.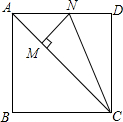 如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=67.5°.
如图,已知正方形ABCD中,CM=CD,MN⊥AC,连接CN,则∠MNC=67.5°.
分析 根据HL先证明两个直角△NMC和直角△NDC全等,得出∠DCN=∠MCN,再根据三角形的内角和定理即可求出∠MNC的度数.
解答 解:∵正方形ABCD中,
∴∠DCA=45°,∠NDC=90°,
∵MN⊥AC,
∴∠NMC=90°,
在Rt△NMC和Rt△NDC中,
$\left\{\begin{array}{l}{CM=CD}\\{NC=CN}\end{array}\right.$,
∴Rt△NMC≌Rt△NDC(HL),
∴∠DCN=∠MCN,
∴∠DCN=∠MCN=22.5°,
∴∠MNC=67.5°;
故答案为:67.5°.
点评 本题主要考查了正方形的性质及直角三角形的全等判定,结合已知和图形,准确找到全等三角形全等需要的条件是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.将数412000用科学记数法表示为( )
| A. | 4.12×106 | B. | 4.12×105 | C. | 41.2×104 | D. | 0.412×106 |
14.下列各式中,错误的是( )
| A. | $\sqrt{25}$=5 | B. | ±$\sqrt{64}$=±8 | C. | $\sqrt{(-6)^{2}}$=-6 | D. | $\root{3}{-8}$=-2 |
4.下面①②③④图形中,含有可以只用一个大写字母表示角的图形是( )


| A. | ①② | B. | ②③ | C. | ②④ | D. | ①④ |
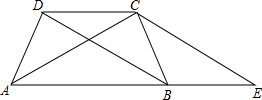 已知:如图,梯形ABCD中,DC∥AB,AD=BC=DC,AC、BD是对角线,E是AB延长线上一点,且∠BCE=∠ACD,联结CE.
已知:如图,梯形ABCD中,DC∥AB,AD=BC=DC,AC、BD是对角线,E是AB延长线上一点,且∠BCE=∠ACD,联结CE.