题目内容
12.声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表:| 气温x/℃ | 0 | 5 | 10 | 15 | 20 |
| 音速y(米/秒) | 331 | 334 | 337 | 340 | 343 |
(2)当气温为22℃时,某人看到烟花燃烧5秒后才听到声响,求此人与烟花燃放所在地的距离为1721米.
分析 (1)先设函数解析式为y=kx+b,根据题意取2组x,y的值代入利用待定系数法求解即可;
(2)把x的值代入(1)中所求的代数式可求出对应的y值,从而判断此人与烟花燃放所在地的距离.
解答 解:(1)设y=kx+b,则
$\left\{\begin{array}{l}{b=331}\\{5k+b=334}\end{array}\right.$,
∴y=$\frac{3}{5}$x+331;
故答案为:y=$\frac{3}{5}$x+331;
(2)∵当x=22时,y=$\frac{3}{5}$x+331,
∴距离为$344\frac{1}{5}×5=1721$(米)
答:此人与烟花燃放所在地的距离为1721米.
故答案为:1721米.
点评 此题主要考查利用一次函数的模型解决实际问题的能力和读图能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解,并会根据图示得出所需要的信息.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
2.对于任意的正数m、n定义运算※为:m?n=$\left\{\begin{array}{l}{\sqrt{m}-\sqrt{n}(m≥n)}\\{\sqrt{m}+\sqrt{n}(m<n)}\end{array}\right.$,计算(3?2)+(8?12)的结果为( )
| A. | $\sqrt{3}$+$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$+3$\sqrt{3}$ | D. | $\sqrt{3}$-$\sqrt{2}$ |
17. 如图,在等腰梯形ABCD中AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是( )
如图,在等腰梯形ABCD中AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是( )
 如图,在等腰梯形ABCD中AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是( )
如图,在等腰梯形ABCD中AD=6cm,BD=9cm,AB=8cm,E、F、G、H分别是AD、BD、BC、AC的中点,那么四边形EFGH的周长是( )| A. | 14cm | B. | 15cm | C. | 16cm | D. | 17cm |
1.在△ABC中,∠C=90°,AB=5,BC=3,则sinB=( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
 如图,点D是△ABC的BC边上的一点,已知AB=13,AD=12,AC=20,BD=5,求BC的长.
如图,点D是△ABC的BC边上的一点,已知AB=13,AD=12,AC=20,BD=5,求BC的长.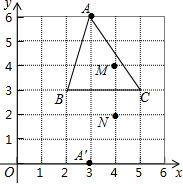 如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).
如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).