题目内容
2.对于任意的正数m、n定义运算※为:m?n=$\left\{\begin{array}{l}{\sqrt{m}-\sqrt{n}(m≥n)}\\{\sqrt{m}+\sqrt{n}(m<n)}\end{array}\right.$,计算(3?2)+(8?12)的结果为( )| A. | $\sqrt{3}$+$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{2}$+3$\sqrt{3}$ | D. | $\sqrt{3}$-$\sqrt{2}$ |
分析 先利用新定义得到原式=$\sqrt{3}$-$\sqrt{2}$+$\sqrt{8}$+$\sqrt{12}$,然后把各二次根式化为最简二次根式后合并即可.
解答 解:(3?2)+(8?12)=$\sqrt{3}$-$\sqrt{2}$+$\sqrt{8}$+$\sqrt{12}$
=$\sqrt{3}$-$\sqrt{2}$+2$\sqrt{2}$+2$\sqrt{3}$
=$\sqrt{2}$+3$\sqrt{3}$.
故选C.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
14. 如图,三角形ABC经过平移得到三角形DEF,则图中平行的线段共有( )
如图,三角形ABC经过平移得到三角形DEF,则图中平行的线段共有( )
 如图,三角形ABC经过平移得到三角形DEF,则图中平行的线段共有( )
如图,三角形ABC经过平移得到三角形DEF,则图中平行的线段共有( )| A. | 0组 | B. | 3组 | C. | 6组 | D. | 9组 |
11.下列各式正确的是( )
| A. | (a+b)2=a2+b2 | B. | (x+6)(x-6)=x2-6 | C. | (x+2)2=x2+2x+4 | D. | (x-y)2=(y-x)2 |
12.声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表:
(1)请直接写出y与x的关系式为y=$\frac{3}{5}$x+331.
(2)当气温为22℃时,某人看到烟花燃烧5秒后才听到声响,求此人与烟花燃放所在地的距离为1721米.
| 气温x/℃ | 0 | 5 | 10 | 15 | 20 |
| 音速y(米/秒) | 331 | 334 | 337 | 340 | 343 |
(2)当气温为22℃时,某人看到烟花燃烧5秒后才听到声响,求此人与烟花燃放所在地的距离为1721米.
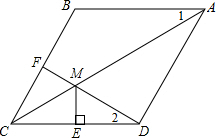 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.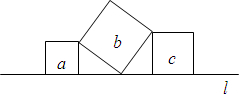 如图,直线l上有三个正方形a,b,c,若a,b的面积分别为5和6,则c的面积为1.
如图,直线l上有三个正方形a,b,c,若a,b的面积分别为5和6,则c的面积为1. 如图,已知AB∥CD,EF分别交AB,CD于点E,F,FG平分∠DFE,交AB于点G,若∠AEF=120°,则∠EFG的度数为60°.
如图,已知AB∥CD,EF分别交AB,CD于点E,F,FG平分∠DFE,交AB于点G,若∠AEF=120°,则∠EFG的度数为60°.