题目内容
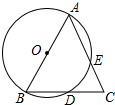在△ABC中，AB=AC，以AB为直径的圆O分别交BC、AC于点D、E， |
| BD |
考点：圆周角定理,等腰三角形的性质
专题：
分析：连接AD，根据
=40°，可得∠BAD=20°，从而求出∠ABC，根据等腰三角形的性质，可得∠BAC的度数．
|
| BD |
解答：解：连接AD，则∠ADB=90°，
，
∵
=40°，
∴∠BAD=20°，
∴∠ABD=70°，
又∵△ABC是等腰三角形，
∴∠BAC=40°．
，∵
|
| BD |
∴∠BAD=20°，
∴∠ABD=70°，
又∵△ABC是等腰三角形，
∴∠BAC=40°．
点评：本题考查了圆周角定理，解答本题的关键是掌握圆周角定理的内容及等腰三角形的性质．
练习册系列答案
教材全解字词句篇系列答案
相关题目
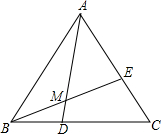如图，D为△ABC中BC上一点，E为AC上一点，连接AD，BE交于点M，满足AM：MD=3：1，BD：DC=2：3，则AE：EC=
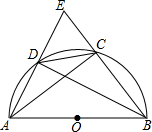如图：AB是半圆的直径，∠ABC的平分线交半圆于D，AD和BC的延长线交于圆外一点E，连结CD．
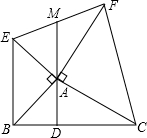如图，在△ABC中，以AB、AC为直角边，分别向外作等腰Rt△ABE和等腰Rt△ACF，连接EF，过点A作AD⊥BC，垂足为D，反向延长DA交EF于点M．把下列各数填在相应的集合里：
17，-
，-21，0，0.35，-6.28，1，10%，
正整数集合：{ }
负整数集合：{ }
正分数集合：{ }
负分数集合：{ }
整数集合：{ }
有理数集合：{ }．
17，-
| 3 |
| 4 |
| 1 |
| 5 |
正整数集合：{ }
负整数集合：{ }
正分数集合：{ }
负分数集合：{ }
整数集合：{ }
有理数集合：{ }．
无论a取什么数，下列算式中有意义的是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
点A（-1，-2）的位置在平面直角坐标系的（ ）
| A、在x轴上 | B、在y轴上 |
| C、在第三象限 | D、在第四象限 |