题目内容
4.大学生小李毕业后回乡自主创业投资办养猪场,分成成猪和仔猪两个互不相邻的正方形猪场,已知成猪场的面积比仔猪场的面积大40m2,两个猪场围墙总长80m,求仔猪场的面积.分析 设小猪场的边长为xm,则大猪场的边长为ym,于是小猪场的面积为x2,大猪场的面积为y2,根据题意,得y2-x2=40,解此方程组即可.
解答 解:设小猪场的边长为xm,则大猪场的边长为ym,
可得:$\left\{\begin{array}{l}{x^2}-{y^2}=40\\ 4x+4y=80\end{array}\right.\begin{array}{l}{\;}&①\\{\;}&②\end{array}$
由①得(x+y)(x-y)=40
由②得x+y=20
∴x-y=2
∴$\left\{\begin{array}{l}x=11\\ y=9\end{array}\right.$
∴112=121,92=81
∴成猪场的面积为121m2,仔猪场的面积为81m2.
点评 此题是一道一元二次方程的应用题,考查了正方形的周长、面积公式以及平方差公式等知识点.

练习册系列答案
相关题目
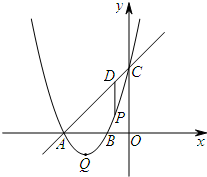 如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(-2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的左侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交直线AC于点D.
如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(-2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的左侧),点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交直线AC于点D.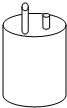 如图:两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是该铁棒的$\frac{1}{3}$,另一根露出水面的长度是该铁棒的$\frac{1}{4}$,两根铁棒长度之和为51厘米,求此木桶中水的深度是多少厘米?
如图:两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是该铁棒的$\frac{1}{3}$,另一根露出水面的长度是该铁棒的$\frac{1}{4}$,两根铁棒长度之和为51厘米,求此木桶中水的深度是多少厘米?