题目内容
1.四边形ABCD的对角线相交于点O,且OA=OB=OC=OD,则它是矩形;若∠AOB=60°,则AB:AC=1:2.分析 求出AC=BD,根据矩形的判定得出即可,求出△AOB是等边三角形,求出AB=AO,即可得出答案.
解答 解:
∵OA=OB=OC=OD,
∴AC=BD,
∴四边形ABCD是矩形;
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴AB=AO=BO=$\frac{1}{2}$AC,
∴AB:AC=1:2,
故答案为:矩,1:2.
点评 本题考查了矩形的判定,等边三角形的性质和判定的应用,能正确运用知识点进行推理是解此题的关键.

练习册系列答案
相关题目
9.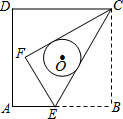 如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
 如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )| A. | 4$\sqrt{3}$ | B. | $\frac{8}{3}$$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{3}$ |
6.方程(1)3x-1=0,(2)2x2-1=0,(3)x2+$\frac{1}{x}$=0,(4)ax2-1=2x(a为实数),(5)x2-1=(x-1)(x-2),其中一元二次方程的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.设a=$\sqrt{5}+1$,a在两个相邻整数之间,则这两个整数是( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
 如图,AD=$\frac{2}{5}$BD,E是BC的中点,BE=2cm,AC=11cm,求线段DE的长.
如图,AD=$\frac{2}{5}$BD,E是BC的中点,BE=2cm,AC=11cm,求线段DE的长.