题目内容
5.在平面直角坐标系中,抛物线y=-$\frac{1}{2}$(x+1)2-$\frac{1}{2}$的顶点是( )| A. | (-1,-$\frac{1}{2}$) | B. | (-1,$\frac{1}{2}$) | C. | (1,-$\frac{1}{2}$) | D. | (1,$\frac{1}{2}$) |
分析 结合抛物线的解析式和二次函数的性质即可得出该抛物线顶点坐标.
解答 解:∵抛物线的解析式为y=-$\frac{1}{2}$(x+1)2-$\frac{1}{2}$,
∴该抛物线的顶点坐标为(-1,-$\frac{1}{2}$).
故选A.
点评 本题考查了二次函数的性质,解题的关键是根据二次函数的性质直接写出抛物线的顶点坐标.本题属于基础题,难度不大,解决该题型题目时,利用配方法将二次函数解析式变形为顶点式是关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
13.对于数据:6,3,4,7,6,0,9,下列判断中正确的是( )
| A. | 这组数据的平均数是6,中位数是6 | B. | 这组数据的平均数是5,中位数是6 | ||
| C. | 这组数据的平均数是6,中位数是7 | D. | 这组数据的平均数是5,中位数是7 |
10.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a3)2=a9 | C. | (-$\frac{1}{2}$)-2=4 | D. | (sin30°-π)0=0 |

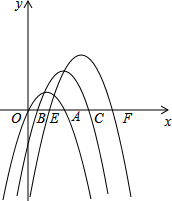 已知,如图,将抛物线y1=-(x-1)2+1,y2=-(x-2)2+2,y3=-(x-3)2+3,…,yn=-(x-n)2+n(n为正整数)称为“系列抛物线”,其分别与x轴交于点O,A,B,C,E,F,….
已知,如图,将抛物线y1=-(x-1)2+1,y2=-(x-2)2+2,y3=-(x-3)2+3,…,yn=-(x-n)2+n(n为正整数)称为“系列抛物线”,其分别与x轴交于点O,A,B,C,E,F,….