题目内容
15.已知关于x的一元二次方程x2+2x+2k-4=0有两个不相等的实数根,且k和方程的根均为整数,则k=±2、-10、-22、-38(无数个).分析 根据方程有两个不相等的实数根结合根的判别式即可得出△=20-8k>0,解不等式即可得出k的取值范围,再根据k和方程的根均为整数,即可得出结论.
解答 解:∵关于x的一元二次方程x2+2x+2k-4=0有两个不相等的实数根,
∴△=22-4×1×(2k-4)=20-8k>0,
解得:k<$\frac{5}{2}$.
∵k和方程的根均为整数,
∴$\sqrt{20-8k}$为偶数,
∴k=±2,k=-10,k=-22,k=-38,…,
故答案为:±2、-10、-22、-38(无数个).
点评 本题考查了根的判别式以及解一元一次不等式,解题的关键是根据方程有两个不相等的实数根得出关于k的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式得出不等式(或方程)是关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
5.盐阜商场试销一种品牌服装,成本为每件300元,规定试销期间销售单价不低于成本单价,且获利不得高于20%,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
| 销售单价x(元) | … | 330 | 335 | 340 | 345 | … |
| 销售量y(件) | … | 240 | 230 | 220 | 210 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
10.下列各数中,最小的数是( )
| A. | -2 | B. | 0 | C. | $\sqrt{2}$ | D. | 3 |
5.在平面直角坐标系中,抛物线y=-$\frac{1}{2}$(x+1)2-$\frac{1}{2}$的顶点是( )
| A. | (-1,-$\frac{1}{2}$) | B. | (-1,$\frac{1}{2}$) | C. | (1,-$\frac{1}{2}$) | D. | (1,$\frac{1}{2}$) |
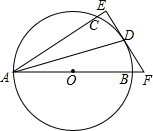 如图,AB是⊙O的直径,点C、D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于点E,与AB的延长线相交于点F.
如图,AB是⊙O的直径,点C、D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于点E,与AB的延长线相交于点F. 如图,过正五边形ABCDE的顶点A作直线AF∥CD,则∠EAF的度数为36°.
如图,过正五边形ABCDE的顶点A作直线AF∥CD,则∠EAF的度数为36°.