题目内容
7. 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为2$\sqrt{2}$的圆与直线OA的位置关系是相离.
如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为2$\sqrt{2}$的圆与直线OA的位置关系是相离.
分析 求出CD的长,根据直线和圆的位置关系判断即可.
解答 解:过C作CD⊥OA于D,
∵∠O=30°,OC=6,
∴CD=$\frac{1}{2}$OC=3,
∵⊙C的半径为2$\sqrt{2}$,即d>r,
∴⊙C和OA的位置关系是相离.
故答案为:相离.
点评 本题考查了直线和圆的位置关系和含30°角的直角三角形性质的应用,能理解直线和圆的位置关系的内容是解此题的关键.

练习册系列答案
相关题目
17.在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
| A. | 4cm | B. | 5cm | C. | 7cm | D. | 14cm |
12.如图图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图案中白色正方形的个数为( )
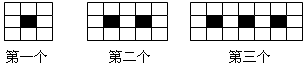

| A. | 50 | B. | 53 | C. | 55 | D. | 60 |
4.下列运算中,正确的是( )
| A. | x•x3=x3 | B. | (x2)3=x5 | C. | x6÷x2=x4 | D. | (x-y)2=x2-y2 |