题目内容
18.有规律排列的一列数:-1、$\frac{3}{4}$、-$\frac{2}{3}$、$\frac{5}{8}$、-$\frac{3}{5}$、…,其中从左到右第100个数是$\frac{101}{200}$.分析 根据题目中数据,可以先进行变形,从而可以发现这组数据的变化规律,从而可以解答本题.
解答 解:∵一列数:-1、$\frac{3}{4}$、-$\frac{2}{3}$、$\frac{5}{8}$、-$\frac{3}{5}$、…,
∴这列数是:$-\frac{2}{2}$、$\frac{3}{4}$、$-\frac{4}{6}$、$\frac{5}{8}$、$-\frac{6}{10}$、…,
∴从左到右第100个数是:$\frac{101}{2×100}$=$\frac{101}{200}$,
故答案为:$\frac{101}{200}$.
点评 本题考查数字的变化类,解题的关键是明确题意,找出数字的变化规律.

练习册系列答案
相关题目
6.下列各数:$\frac{1}{7}$,-π,-$\sqrt{3}$,0.$\stackrel{•}{3}$,-0.1010010001…(两个1之间依次多一个0),-$\sqrt{49}$中无理数的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
13.下列四个数中最大的是( )
| A. | -2 | B. | 0 | C. | -$\frac{3}{5}$ | D. | 0.7 |
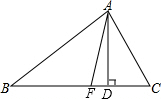 如图,AD,AF分别是△ABC的高和角平分线,已知∠B=36°,∠C=76°,则∠DAF=20°.
如图,AD,AF分别是△ABC的高和角平分线,已知∠B=36°,∠C=76°,则∠DAF=20°.
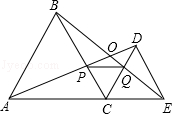 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下三个结论:①AD=BE;②EQ=DP;③△CPQ是等边三角形;其中一定成立的结论有①②③.
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下三个结论:①AD=BE;②EQ=DP;③△CPQ是等边三角形;其中一定成立的结论有①②③. 如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为2$\sqrt{2}$的圆与直线OA的位置关系是相离.
如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为2$\sqrt{2}$的圆与直线OA的位置关系是相离.