题目内容
在平面直角坐标系中,直线L:y=
x-
交坐标轴于A,B两点(A点在x正半轴上,B点在y轴负半轴上),点C为(1,0),在直线L上是否存在点P,使得△POC为等腰三角形?若存在,求出所有可能的点,否则请说明理由.
| 1 |
| 3 |
| 4 |
| 3 |
考点:一次函数综合题
专题:
分析:根据函数解析式,可得直线上的点的坐标,根据等腰三角形的定义,分类讨论:①OP=PC,②OC=OP=1,③PC=OC=1,根据两点间的距离,可得关于a的方程,根据解方程,可得答案.
解答:解:在直线L上存在点P,使得△POC为等腰三角形,
由P在直线L上,得P(a,
a-
).
①当OP=PC时,平方得(a-1)2+(
a-
)2=a2+(
a-
)2.
化简,得2a=1,解得a=
,
a-
=-
,即P1(
,-
);
②当OC=OP=1时,平方得a2+(
a-
)2=1.化简得
10a2-8a+7=0,△=(-8)2-4×10×7=-216<0,
不存在实数a,即P点不存在;
③当PC=OC=1时,平方得(a-1)2+(
a-
)2=1.
化简得5a2-13a+8=0.因式分解,得
(5a-8)(a-1)=0.
解得a=
或a=1.
当a=1时,
a-
=-1,即P2(1,-1).
当a=
时,
a-
=-
,即P3(
,-
),
综上所述:P1(
,-
),P2(1,-1),P3(
,-
),使得△POC为等腰三角形.
由P在直线L上,得P(a,
| 1 |
| 3 |
| 4 |
| 3 |
①当OP=PC时,平方得(a-1)2+(
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
化简,得2a=1,解得a=
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| 7 |
| 6 |
| 1 |
| 2 |
| 7 |
| 6 |
②当OC=OP=1时,平方得a2+(
| 1 |
| 3 |
| 4 |
| 3 |
10a2-8a+7=0,△=(-8)2-4×10×7=-216<0,
不存在实数a,即P点不存在;
③当PC=OC=1时,平方得(a-1)2+(
| 1 |
| 3 |
| 4 |
| 3 |
化简得5a2-13a+8=0.因式分解,得
(5a-8)(a-1)=0.
解得a=
| 8 |
| 5 |
当a=1时,
| 1 |
| 3 |
| 4 |
| 3 |
当a=
| 8 |
| 5 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 8 |
| 5 |
| 4 |
| 5 |
综上所述:P1(
| 1 |
| 2 |
| 7 |
| 6 |
| 8 |
| 5 |
| 4 |
| 5 |
点评:本题考查了一次函数的综合题,利用点在函数图象上设出点的坐标,分类讨论:①OP=PC,②OC=OP=1,③PC=OC=1,再解方程求出P点的坐标.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
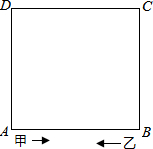 如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米,
如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米, 如图,圆内接四边形对角线AB⊥CD于P,OE⊥AD于E,OE=2,则BC=
如图,圆内接四边形对角线AB⊥CD于P,OE⊥AD于E,OE=2,则BC=