题目内容
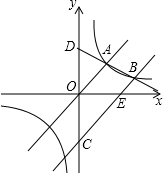 已知直线OA:y1=k1x与双曲线y2=
已知直线OA:y1=k1x与双曲线y2=| k2 |
| x |
(1)求直线和双曲线的解析式;
(2)将直线OA沿y轴向下平移,交y轴于点C,交双曲线于点B,直线BA交y轴于点D,若O恰好是CD的中点,求平移后直线BC的解析式.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)将点A的坐标代入反比例函数解析式和一次函数解析式,利用待定系数法求直线解析式解答;
(2)根据平移的特点,设出平移后相对应的解析式,然后求得此解析式与直线BC的交点B的坐标,代入反比例函数的解析式,即可求得位置系数,从而求解.
(2)根据平移的特点,设出平移后相对应的解析式,然后求得此解析式与直线BC的交点B的坐标,代入反比例函数的解析式,即可求得位置系数,从而求解.
解答:解:(1)将A(2,2)分别代入y1=k1x与双曲线y2=
得:2=2k1,所以k1=1,所以y1=x;
2=
,
∴k2=4,
则解析式分别为:y1=x,y2=
.
(2)∵y1=x,
∴∠DOA=45°,
∵OA∥BC,
∴∠DOA=∠OCE=45°,
∴△OCE是等腰直角三角形,
设向下平移m个单位,则直线BC的解析式为y=x-m,
且OC=OD=OE=m,
∴E点坐标是(m,0),D的坐标是(0,m),
设直线AB的解析式是y=kx+b,
则
,
解得:
,
则直线AB的解析式是:y=(1-
)x+m,
解方程组
,
解得:
,
即B的坐标是(4,4-m),代入y=
得:4(4-m)=4,
解得:m=3,
则直线BC的解析式是:y=x-3.
| k2 |
| x |
得:2=2k1,所以k1=1,所以y1=x;
2=
| k2 |
| 2 |
∴k2=4,
则解析式分别为:y1=x,y2=
| 4 |
| x |
(2)∵y1=x,
∴∠DOA=45°,
∵OA∥BC,
∴∠DOA=∠OCE=45°,
∴△OCE是等腰直角三角形,
设向下平移m个单位,则直线BC的解析式为y=x-m,
且OC=OD=OE=m,
∴E点坐标是(m,0),D的坐标是(0,m),
设直线AB的解析式是y=kx+b,
则
|
解得:
|
则直线AB的解析式是:y=(1-
| m |
| 2 |
解方程组
|
解得:
|
即B的坐标是(4,4-m),代入y=
| 4 |
| x |
得:4(4-m)=4,
解得:m=3,
则直线BC的解析式是:y=x-3.
点评:本题考查了反比例函数图象与一次函数图象的交点问题,根据已知条件先判断出点A的横坐标是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
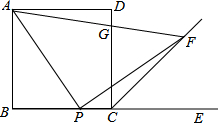 如图,在正方形ABCD中,AB=2,点P是边BC上的任意一点,E是BC延长线上一点,联结AP,作PF⊥AP交∠DCE的平分线CF上一点F,联结AF交边CD于点G.
如图,在正方形ABCD中,AB=2,点P是边BC上的任意一点,E是BC延长线上一点,联结AP,作PF⊥AP交∠DCE的平分线CF上一点F,联结AF交边CD于点G.