题目内容
16.解方程组(1)$\left\{\begin{array}{l}y=2x-5\\ 7x-3y=20\end{array}\right.$
(2)$\left\{\begin{array}{l}\frac{x}{2}-\frac{y+1}{3}=1\\ 3x+2y=10\end{array}\right.$
(3)$\left\{\begin{array}{l}\frac{x+1}{3}=2y\\ 2({x+1})-y=11\end{array}\right.$
(4)$\left\{\begin{array}{l}19x+18y=17\\ 17x+16y=15\end{array}\right.$.
分析 (1•)方程组利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可;
(3)方程组整理后,利用代入消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{y=2x-5①}\\{7x-3y=20②}\end{array}\right.$,
把①代入②得:7x-6x+15=20,
解得:x=5,
把x=5代入①得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=5}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{3x-2y=8①}\\{3x+2y=10②}\end{array}\right.$,
①+②得:6x=18,
解得:x=3,
①-②得:-4y=-2,
解得:y=$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=\frac{1}{2}}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{\frac{x+1}{3}=2y①}\\{2(x+1)-y=11②}\end{array}\right.$,
由①得:x+1=6y③,
把③代入②得:12y-y=11,
解得:y=1,
把y=1代入③得:x=5,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{19x+18y=17①}\\{17x+16y=15②}\end{array}\right.$,
①×17-②×19得:2y=4,
解得:y=2,
把y=2代入①得:x=-1,
则方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案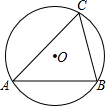 如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )
如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
| A. | 3 | B. | -3 | C. | ±3 | D. | ±2 |
| A. | 2 | B. | -2 | C. | 2或-6 | D. | -2或-6 |
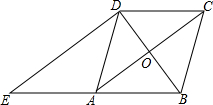 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.