题目内容
7.在平面直角坐标系中,以点(1,1)为圆心$\sqrt{5}$为半径作圆O,则圆O与坐标轴的交点坐标是(0,3)、(0,-1)、(3,0)、(-1,0).分析 如图,设⊙P与坐标轴分别交于A、B、C、D.作PE⊥OA于E,PF⊥OD于F.易知四边形PEOF是正方形,边长为1,由勾股定理可得AE=DF=BF=CE=2,由此即可解决问题.
解答 解:如图,设⊙P与坐标轴分别交于A、B、C、D.作PE⊥OA于E,PF⊥OD于F.
易知四边形PEOF是正方形,边长为1,
由勾股定理可得AE=DF=BF=CE=2,
∴A(0,3),B(-1,0),C(0,-1),D(3,0),
故答案为(0,3)、(0,-1)、(3,0)、(-1,0);
点评 本题考查勾股定理、直线与圆的位置关系、正方形的判定、坐标与图象的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4. 如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
 如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )| A. | $\frac{2\sqrt{5}}{3}$ | B. | 1 | C. | $\frac{3\sqrt{17}}{17}$ | D. | $\frac{4\sqrt{17}}{17}$ |
19.已知∠AOB=30°,自∠AOB顶点O引射线OC,若∠AOC:∠AOB=4:3,那么∠BOC的度数是( )
| A. | 10° | B. | 40°或30° | C. | 70° | D. | 10°或70° |
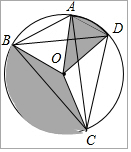 已知四边形ABCD是⊙O的内接垂直四边形,AB=3,CD=4,连接OA,OB,OC,OD,求图中扇形AOD和扇形BOC面积的和(图中阴影部分).
已知四边形ABCD是⊙O的内接垂直四边形,AB=3,CD=4,连接OA,OB,OC,OD,求图中扇形AOD和扇形BOC面积的和(图中阴影部分). 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,AB=6,AC=10,则AE=8.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,AB=6,AC=10,则AE=8.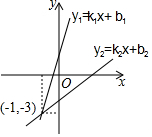 如图,平面直角坐标系xOy中,直线y1=k1x+b1的图象与直线y2=k2x+b2的图象相交于点(-1,-3),当y1<y2时,实数x的取值范围为x<-1.
如图,平面直角坐标系xOy中,直线y1=k1x+b1的图象与直线y2=k2x+b2的图象相交于点(-1,-3),当y1<y2时,实数x的取值范围为x<-1.