题目内容
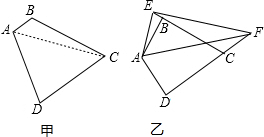
10.有一个四边形ABCD,BC=CD,∠BCD=60°,∠BAD=120°.(1)小明认为AB+AD=AC(如图甲),为了证明它,需要作辅助线,请问需要怎样作辅助线?小明认为作完辅助线后,还要证明一对三角形全等,请指出这一对三角形;
(2)若AB=AD(如图乙),F是DC延长线上一点,作∠FAE=60°,AE与CB的延长线交点为E,连EF,线段EF、EB和DF之间有怎样的数量关系?请说明理由.
分析 (1)先判断出△ADG和BCD是等边三角形,得出∠BDG=∠CDA,即可得出结论;
(2)先判断出△ABC≌△ADC,结合四边形的内角和得出∠ABC=∠ADC=90°,再判断出△ADE'≌△ABE得出AE'=AE,最后判断出△EAF≌△E'AF即可.
解答 解:(1)△BDG≌△CDA;
如图甲,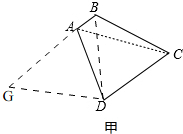
连接BD,延长BA至G,使AG=AD,
∵∠BAD=120°,
∴∠DAG=60°,
∵AG=AD,
∴△ADG是等边三角形,
∴∠ADG=60°,DG=AD,
∵∠BCD=60°,BC=CD,
∴△BCD是等边三角形,
∴∠BDC=60°,BD=CD,
∴∠BDG=∠CDA,
在△BDG和△CDA中,$\left\{\begin{array}{l}{BD=CD}\\{∠BDG=∠CDA}\\{DG=AD}\end{array}\right.$,
∴△BDG≌△CDA,
∴AC=BG=AG+AB=AD+AB,
(2)DF=EB+EF,
理由:如图乙,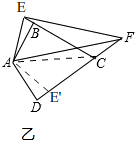
在四边形ABCD中,∠BAD=120°∠BCD=60°,
根据四边形的内角和得,∠ABC+∠ADC=180°
在△ABC和△ADC中,$\left\{\begin{array}{l}{AB=AD}\\{BC=CD}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC,
∴∠ABC=∠ADC=90°,∠BAC=∠DAC=60°,
∵∠EAF=60°,
∴∠EAB=∠CAF
在△ACD内部作∠DAE'=∠BAE,
∴∠CAF=∠DAE',
∴∠FAE'=∠FAC+∠CAE'=∠DAE'+∠CAE'=60°=∠EAF,
在△ADE'和△ABE中,$\left\{\begin{array}{l}{∠ADE'=∠ABE=90°}\\{AD=AB}\\{∠DAE'=∠BAE}\end{array}\right.$,
∴△ADE'≌△ABE,
∴AE'=AE,
在△EAF和△E'AF中,$\left\{\begin{array}{l}{AE=AE'}\\{∠EAF=∠E'AF}\\{AF=AF}\end{array}\right.$,
∴△EAF≌△E'AF,
∴EF=E'F,
∴DF=DE'+E'F=EB+EF.
点评 此题是三角形综合题,主要考查了四边形的内角和,等边三角形的判定和性质,全等三角形的判定和性质,解本题的关键是作出辅助线△ACD内部作∠DAE'=∠BAE,也是解本题的难点.


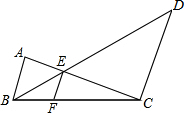 如图:AB∥EE∥CD,AB=3,CD=5,则EF的长=$\frac{15}{8}$.
如图:AB∥EE∥CD,AB=3,CD=5,则EF的长=$\frac{15}{8}$.