题目内容
 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=8,AC=6,DE=4,则△ABC的面积为( )
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=8,AC=6,DE=4,则△ABC的面积为( )| A、56 | B、32 | C、28 | D、24 |
考点:角平分线的性质
专题:
分析:由角平分线的性质可知DE=DF=4,再利用S△ABC=S△ABD+S△ADC可求得△ABC的面积.
解答:解:
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DF=DE=4,
∴S△ABC=S△ABD+S△ADC=
AB•DE+
AC•DF=
×8×4+
×6×4=16+12=28,
故选C.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DF=DE=4,
∴S△ABC=S△ABD+S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题主要考查角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键.

练习册系列答案
相关题目
⊙O的半径为4cm,点P和圆心的距离为8cm,则过P点的⊙O的两条切线的夹角是( )
| A、30° | B、60° |
| C、90° | D、120° |
下面四个方程中,与方程x-1=2的解相同的一个是( )
| A、2x=6 |
| B、x+2=-1 |
| C、2x+1=3 |
| D、-3x=9 |
 如图,已知正方形ABCD的边长为8,点E,F分别在边BC、CD上,∠EAF=45°.当EF=8时,△AEF的面积是( )
如图,已知正方形ABCD的边长为8,点E,F分别在边BC、CD上,∠EAF=45°.当EF=8时,△AEF的面积是( )| A、8 | B、16 | C、24 | D、32 |
已知三角形的两边长分别为3和6,则下列长度的线段能作为第三边的是( )
| A、3 | B、6 | C、9 | D、12 |
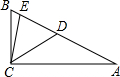 在△ABC中,∠ACB=90°,D、E在AB上,且BD=BC,AE=AC,则∠DCE的度数为
在△ABC中,∠ACB=90°,D、E在AB上,且BD=BC,AE=AC,则∠DCE的度数为