题目内容
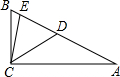 在△ABC中,∠ACB=90°,D、E在AB上,且BD=BC,AE=AC,则∠DCE的度数为
在△ABC中,∠ACB=90°,D、E在AB上,且BD=BC,AE=AC,则∠DCE的度数为考点:等腰三角形的性质
专题:
分析:利用等边对等角找到∠CDE、∠CED和∠ECD之间的关系,再利用∠ACB=90°和三角形内角和可得到关于∠ECD的方程,求得即可.
解答:解:∵BD=BC,AE=AC,
∴∠BCD=∠BDC,∠AEC=∠ACE,
即∠BCE+∠DCE=∠BDC,∠ACD+∠DCE=∠CDE,
∵∠DCE+∠BDC+∠AEC=180°,
∴∠BCE+∠DCE+∠ACD+∠DCE+∠DCE=180°,
又∠ACB=90°,
∴∠BCE+∠DCE+∠ACD=90°,
∴2∠DCE=180°-90°,
∴∠DCE=45°,
故答案为:45°.
∴∠BCD=∠BDC,∠AEC=∠ACE,
即∠BCE+∠DCE=∠BDC,∠ACD+∠DCE=∠CDE,
∵∠DCE+∠BDC+∠AEC=180°,
∴∠BCE+∠DCE+∠ACD+∠DCE+∠DCE=180°,
又∠ACB=90°,
∴∠BCE+∠DCE+∠ACD=90°,
∴2∠DCE=180°-90°,
∴∠DCE=45°,
故答案为:45°.
点评:本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和这一隐含条件的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=8,AC=6,DE=4,则△ABC的面积为( )
如图,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=8,AC=6,DE=4,则△ABC的面积为( )| A、56 | B、32 | C、28 | D、24 |
已知一个圆锥形零件的母线长为3,底面半径为2,则这个圆锥形的零件的侧面积为( )
| A、2π | B、5π | C、3π | D、6π |
如果代数式3x+5与2x-3的值互为相反数,则x的值应为( )
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
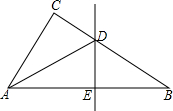 如图,△ABC中,∠C=90°,AB的中垂线DE交AB于E,交BC于D,若CB=8,AC=6,则△ACD的周长为( )
如图,△ABC中,∠C=90°,AB的中垂线DE交AB于E,交BC于D,若CB=8,AC=6,则△ACD的周长为( )| A、16 | B、14 | C、20 | D、18 |