题目内容
已知三角形的两边长分别为3和6，则下列长度的线段能作为第三边的是（ ）
| A、3 | B、6 | C、9 | D、12 |
考点：三角形三边关系
专题：
分析：△ABC的两边a、b之和是9，a、b之差是3．根据在三角形中任意两边之和＞第三边，任意两边之差＜第三边；即可求第三边长c的范围，然后由c的范围来作出选择．
解答：解：设三角形的两边长分别为a、b，第三边是c．则：
a+b=9、a-b=3，
∴3＜c＜9．
故选：B．
a+b=9、a-b=3，
∴3＜c＜9．
故选：B．
点评：本题考查了三角形三边关系的应用．此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．
练习册系列答案
金博士一点全通系列答案
相关题目
如图，在△ABC中，AD平分∠BAC，DE⊥AB，DF⊥AC，垂足分别为E，F．若AB=8，AC=6，DE=4，则△ABC的面积为（ ）| A、56 | B、32 | C、28 | D、24 |
下列与|-a-b+c|相等的是（ ）
| A、|a-（+b）-（+c）| |
| B、|a-（+b）-（-c）| |
| C、|a-（-b）+（-c）| |
| D、|a+（-b）+（+c）| |
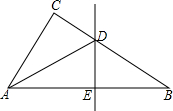如图，△ABC中，∠C=90°，AB的中垂线DE交AB于E，交BC于D，若CB=8，AC=6，则△ACD的周长为（ ）| A、16 | B、14 | C、20 | D、18 |