题目内容
8.已知$\sqrt{x}$=$\sqrt{a}$-$\frac{1}{\sqrt{a}}$,求$\frac{x+2+\sqrt{{x}^{2}+4x}}{x+2-\sqrt{{x}^{2}+4x}}$的值.分析 由$\sqrt{x}$=$\sqrt{a}$-$\frac{1}{\sqrt{a}}$,得出x=a+$\frac{1}{a}$-2,进一步化简代数式代入求得答案即可.
解答 解:∵$\sqrt{x}$=$\sqrt{a}$-$\frac{1}{\sqrt{a}}$,
∴x=a+$\frac{1}{a}$-2,
∴$\frac{x+2+\sqrt{{x}^{2}+4x}}{x+2-\sqrt{{x}^{2}+4x}}$
=$\frac{(x+2+\sqrt{{x}^{2}+4x})^{2}}{(x+2-\sqrt{{x}^{2}+4x})(x+2+\sqrt{{x}^{2}+4x})}$
=$\frac{1}{4}$(x+2+$\sqrt{(x+2)^{2}-4}$)2
=$\frac{1}{4}$(a+$\frac{1}{a}$+a-$\frac{1}{a}$)2
=a2.
点评 此题考查二次根式的化简求值,掌握完全平方公式是解决问题的关键.

练习册系列答案
相关题目
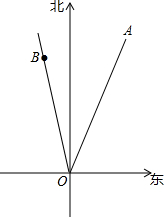 2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响.
2014年第10号台风“麦德姆”,是2014年度对我国破坏性最大的一次台风,“麦德姆”台风从福建登陆后一路北上,在青岛荣成再次登陆.如图所示,某时,台风“麦德姆”的中心在点O沿北偏东20°的方向以30km/h的速度移动,在点O北偏西10°的方向距离O点360km处有一个小岛B.如果台风中心的最大风力为14级,每远离台风中心20千米风力减弱一级,小岛A的风力达到四级或四级以上,则称其受台风影响. 如图,AB、CD是⊙O的直径,弦CE∥AB.$\widehat{BD}$与$\widehat{BE}$相等吗?为什么?
如图,AB、CD是⊙O的直径,弦CE∥AB.$\widehat{BD}$与$\widehat{BE}$相等吗?为什么?