题目内容
将抛物线y=-
x2+bx+c向上平移2个单位,再向右平移1个单位后得到的抛物线为y=-
x2,则b= ,c= .
| 1 |
| 2 |
| 1 |
| 2 |
考点:二次函数图象与几何变换
专题:
分析:先求得每个抛物线的顶点坐标,根据抛物线如何平移,顶点就如何平移可得b+1=0,
+2=0,即可求得b、c的值.
| 2c+b2 |
| 2 |
解答:解:抛物线y=-
x2+bx+c的顶点坐标为(b,
)
抛物线y=-
x2,的顶点坐标为(0,0)
∵将抛物线y=-
x2+bx+c向上平移2个单位,再向右平移1个单位后得到的抛物线为y=-
x2,
∴b+1=0,
+2=0,
∴b=-1,c=-
.
故答案为:-1,-
.
| 1 |
| 2 |
| 2c+b2 |
| 2 |
抛物线y=-
| 1 |
| 2 |
∵将抛物线y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴b+1=0,
| 2c+b2 |
| 2 |
∴b=-1,c=-
| 5 |
| 2 |
故答案为:-1,-
| 5 |
| 2 |
点评:本题主要考查了二次函数图象与几何变换.关键是利用抛物线如何平移,顶点就如何平移.

练习册系列答案
相关题目
 如图,定圆0的半径是3cm,动圆P的半径是lcm,动圆在直线,上移动,当两圆相切时,0P的长是( )cm.
如图,定圆0的半径是3cm,动圆P的半径是lcm,动圆在直线,上移动,当两圆相切时,0P的长是( )cm.| A、2或4 | B、2 | C、4 | D、3 |
 如图,已知△ABC的内切圆O切AC于点K,D是AC的中点,求证:直线DO平分线段BK.
如图,已知△ABC的内切圆O切AC于点K,D是AC的中点,求证:直线DO平分线段BK. 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=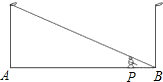 如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为
如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A有20米,离路灯B有5米,如果小亮的身高为1.6米,那么路灯高度为 如图,在△ABC中,DE∥BC,∠A=55°,∠ABC=60°,则∠AED=
如图,在△ABC中,DE∥BC,∠A=55°,∠ABC=60°,则∠AED= 如图,在矩形ABCD中,AD=3,BD=5,则此矩形的周长为
如图,在矩形ABCD中,AD=3,BD=5,则此矩形的周长为