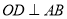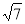题目内容
(本题12分)如图,过点A(0,3)的直线l1与x轴交于点B,tan∠ABO= .过点A的另一直线l2:y=-
.过点A的另一直线l2:y=- x+b (t>0)与x轴交于点Q,点P是射线AB上的一个动点,过P作PH⊥x轴于点H,设PB=5t.
x+b (t>0)与x轴交于点Q,点P是射线AB上的一个动点,过P作PH⊥x轴于点H,设PB=5t.

(1)求直线l1 的函数解析式;
(2)当点P在线段AB上运动时,设△PHQ的面积为S(S≠0),求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)当点P 在射线AB上运动时,是否存在这样的t值,使以P,H,Q为顶点的三角形与△AOQ相似?若存在,直接写出所有满足条件的t值所对应的P点坐标;若不存在,请说明理由.
(1)函数解析式为y=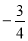 x+3;(2)①当H在Q、B之间时S=
x+3;(2)①当H在Q、B之间时S=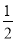 (4-8t)×3t=
(4-8t)×3t=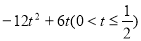 ②当H在O、Q之间时,S=
②当H在O、Q之间时,S=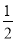 (8t-4) 3t=
(8t-4) 3t=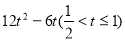 ;(3)t1=
;(3)t1=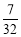 ,P1
,P1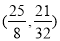 ;t2=
;t2=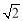 -1,P2
-1,P2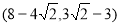 ; t3=
; t3=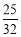 ,P3
,P3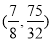 ;t4=1,P4(0,3);t5=1, P5(8,-3)
;t4=1,P4(0,3);t5=1, P5(8,-3)
【解析】
试题分析:(1)∵A(0,3),且tan∠ABO=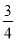 ∴B(4,0)
∴B(4,0)
设y=kx+b ,将A(0,3) B(4,0)代入上式得b=3 0=4k+b
解得k=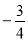 ,b=3
,b=3
∴ 函数解析式为y=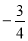 x+3
x+3
(2)由B(4,0).∴OB=4,
∵OA=3, ∴AB=5.
由题意,得△BHP∽△BOA,
∵OA∶OB∶AB=3∶4∶5,
∴HP∶HB∶BP=3∶4∶5,
∵PB=5t,∴HB=4t,HP=3t.
∴OH=OB-HB=4-4t.
由y=-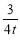 x+3与x轴交于点Q, 得Q(4t,0)
x+3与x轴交于点Q, 得Q(4t,0)
①当H在Q、B之间时(如图1)
QH=OH-OQ=(4-4t)-4t=4-8t.
S=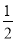 (4-8t)×3t=
(4-8t)×3t=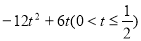
②当H在O、Q之间时(如图2)
QH=OQ-OH=4t-(4-4t)=8t-4.
S=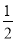 (8t-4) 3t=
(8t-4) 3t=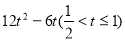
(3)存在t的值,使以P、H、Q为顶点的三角形与△AOQ相似
①当H在Q、B之间
t1=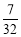 ,P1
,P1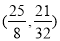 或者t2=
或者t2=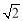 -1,P2
-1,P2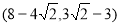
②当H在O、Q之间
t3=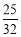 .得P3
.得P3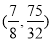 或者t4=1,P4(0,3)
或者t4=1,P4(0,3)
③当H在B的右侧
t5=1, P5(8,-3)


考点:一次函数的综合运用