题目内容
方程x2+
x-1=0的解可视为函数y=x+
的图象与函数y=
的图象交点的横坐标.若方程x4+ax-4=0的各个实根x1,x2,…,xk(k≤4)所对应的点(xi,
)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
| 2 |
| 2 |
| 1 |
| x |
| 4 |
| xi |
考点:反比例函数综合题,反比例函数与一次函数的交点问题
专题:
分析:原方程等价于 x3+a=
,分别作出左右两边函数的图象:分a>0与a<0讨论,可得答案.
| 4 |
| x |
解答:
 解:方程的根显然x≠0,原方程等价于x3+a=
解:方程的根显然x≠0,原方程等价于x3+a=
,
原方程的实根是曲线y=x3+a与曲线y=
的交点的横坐标,
而曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的,
若交点(xi,
)(i=1,2,k)均在直线y=x的同侧,
因直线y=x与y=
交点为:(-2,-2),(2,2);
所以结合图象可得
或
,
解得a>6或a<-6.
故答案为:a>6或a<-6.

 解:方程的根显然x≠0,原方程等价于x3+a=
解:方程的根显然x≠0,原方程等价于x3+a=| 4 |
| x |
原方程的实根是曲线y=x3+a与曲线y=
| 4 |
| x |
而曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的,
若交点(xi,
| 4 |
| xi |
因直线y=x与y=
| 4 |
| x |
所以结合图象可得
|
|
解得a>6或a<-6.
故答案为:a>6或a<-6.
点评:本题综合考查了反比例函数,反比例函数与一次函数图象的交点问题,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质.

练习册系列答案
相关题目
若(x2+x+1)6=a12x12+a11x11+a10x10+…+a1x+a0,则a11+a9+a7+a5+a3+a1=( )
| A、364 | B、365 |
| C、730 | D、728 |
 如图所示,四条双曲线在坐标轴内,则k1,k2,k3,k4的大小关系是( )
如图所示,四条双曲线在坐标轴内,则k1,k2,k3,k4的大小关系是( )| A、k1>k2>k3>k4 |
| B、k2>k1>k4>k3 |
| C、k1>k2>k4>k3 |
| D、k2>k1>k3>k4 |
 样本,绘制成绩统计图如图所示,请结合统计图回答下列问题.
样本,绘制成绩统计图如图所示,请结合统计图回答下列问题.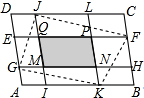 如图,在平行四边形ABCD中,EF∥GH∥AB,IJ∥KL∥BC,若四边形MNPQ的面积为19,四边形GKFL的面积为90,则平行四边形ABCD的面积为
如图,在平行四边形ABCD中,EF∥GH∥AB,IJ∥KL∥BC,若四边形MNPQ的面积为19,四边形GKFL的面积为90,则平行四边形ABCD的面积为