题目内容
直径为1的球内放一个正方体,那么这个正方体的棱长的最大值为 .
考点:二次函数的应用,勾股定理的应用
专题:
分析:利用球与其内接正方体的关系,得出球的半径与其内接正方体边长之间的关系是解决本题的关键,发现球的直径就是其内接正方体的体对角线长.
解答: 解:设这个正方体的棱长的最大值为x,
解:设这个正方体的棱长的最大值为x,
∴A1B=
x=
x,
∴这个正方体的体对角线A1C=
x=
x,
∵球的直径为1,
∴
x=1,
∴x=
.
故答案为:
.
 解:设这个正方体的棱长的最大值为x,
解:设这个正方体的棱长的最大值为x,∴A1B=
| 12+12 |
| 2 |
∴这个正方体的体对角线A1C=
(
|
| 3 |
∵球的直径为1,
∴
| 3 |
∴x=
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查空间几何体的内外接问题,要找准球与其内接正方体之间的联系,建立球的半径与正方体边长之间的关系,体现了转化与化归思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若(x2+x+1)6=a12x12+a11x11+a10x10+…+a1x+a0,则a11+a9+a7+a5+a3+a1=( )
| A、364 | B、365 |
| C、730 | D、728 |
 如图中不同的长方形(包括正方形)的个数为( )
如图中不同的长方形(包括正方形)的个数为( )| A、36 | B、87 | C、72 | D、102 |

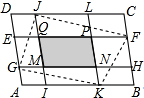 如图,在平行四边形ABCD中,EF∥GH∥AB,IJ∥KL∥BC,若四边形MNPQ的面积为19,四边形GKFL的面积为90,则平行四边形ABCD的面积为
如图,在平行四边形ABCD中,EF∥GH∥AB,IJ∥KL∥BC,若四边形MNPQ的面积为19,四边形GKFL的面积为90,则平行四边形ABCD的面积为