题目内容

直线L1：y=x-1与x轴交于A点，若L1与L2垂直，且垂足是A，则L2的解析式是
 
．
考点：两条直线相交或平行问题
专题：
分析：由于L1与L2垂直，过点A的直线L1的函数解析式为y=x-1，则与直线L1垂直的直线L2的函数解析式为y=-x+b，A点坐标为（1，0），代入方程，即可得出L2的解析式．
解答：解：∵直线L1：y=x-1与x轴交于A点，
∴A点坐标为（1，0），
设直线L2的函数解析式为y=kx+b，
又∵两直线垂直，则k=-1，
又∵因为直线L2过点A，则0=-1+b，
得b=1，
故直线L2的函数解析式为：y=-x+1．
故答案为：y=-x+1．
点评：本题考查了直线互相垂直时两斜率之积为-1的知识点，要求学生对此类题熟练掌握．
练习册系列答案
相关题目
（Ⅰ）如图1，P是⊙O外一点，直线OP交⊙O于A，B两点（PA＞PB）．取⊙O上异于A，B的一点Q，连接PQ．判断PA，PB，PQ的大小关系．
（Ⅱ）如图2，等边△ABC的边长为1，两顶点A，B分别在x轴、y轴上运动，试求OC（O为原点）的最大值．
公园小路如图，只要把A，B，C，D，E，F，G七个点中的
 
两处设为出口，可实现从一口进从另一口出且使游客走完全部小路而又不重复走．
设
1
x2
-x=1，则（1-x5）5+x=
 
．
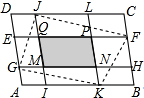如图，在平行四边形ABCD中，EF∥GH∥AB，IJ∥KL∥BC，若四边形MNPQ的面积为19，四边形GKFL的面积为90，则平行四边形ABCD的面积为
 
．
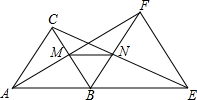如图，△ABC和△BEF都是正三角形，AF与BC交于点M，BF与EC交于点N，则下面三个结论中，正确的结论有
 
个．
（1）AF=CE；
（2）MN∥AE；
（3）AC⊥CE的充分必要条件是AF⊥EF．
用下述方法确定实数对先后顺序，若a1＞b1，或者a1=b1且a2＞b2则称（a1，a2）先于（b1，b2），简记为（a1，a2）＞（b1，b2），则三个实数对A=（
5
+2，
6
+
3
），B=（
6
+
3
，
9+4
5
）C=（
9+4
5
，
5
+2）的先后顺序为
 
．
已知P（-l，a）在反比例函数y=
6
x
的图象上，则a的值为（　　）
A、-lB、-6C、6D、1
定义一种新的运算*，使a*b=ab（a+b），则方程（x*2）*2=96的根为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网