题目内容
15．如果$\frac{\sqrt{x+5}}{\sqrt{3-x}}$在实数范围内有意义，那么x的取值范围是-5≤x＜3．分析 根据二次根式有意义的条件可得x+5≥0，3-x≥0，根据分式有意义的条件可得3-x≠0，进而可得x的取值范围．
解答 解：由题意得：$\left\{\begin{array}{l}{x+5≥0}\\{3-x＞0}\end{array}\right.$，
解得：-5≤x＜3，
故答案为：-5≤x＜3．
点评 此题主要考查了二次根式有意义的条件，关键是掌握二次根式中的被开方数是非负数．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
如图所示，DE是△ABC的中位线，则△ADE与△ABC的周长比为1：2．
20．下列分式中是最简分式的是（ ）
| A． | $\frac{x-1}{{{x^2}-1}}$ | B． | $\frac{4}{2x}$ | C． | $\frac{2x}{{{x^2}-1}}$ | D． | $\frac{1-x}{x-1}$ |
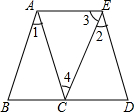已知：如图所示，∠1=∠2，∠3=∠B，AC∥DE，且B，C，D在一条直线上．求证：AE∥BD．
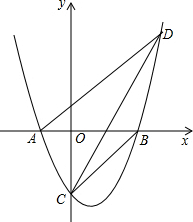已知抛物线y=ax2+bx+c与x轴相交于点A（-1，0）和点B（4，0），与y轴相交于点C（0，-4）