题目内容
3. 如图所示,DE是△ABC的中位线,则△ADE与△ABC的周长比为1:2.
如图所示,DE是△ABC的中位线,则△ADE与△ABC的周长比为1:2.
分析 根据题意DE是△ABC的中位线,那么DE∥BC,再利用平行线分线段成比例定理的推论,可得△ADE∽△ABC,再利用相似三角形的周长比等于相似即可求出答案.
解答 解:∵DE是△ABC的中位线,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{1}{2}$,
根据相似三角形的性质△ADE与△ABC的周长之比是1:2.
故选1:2.
点评 本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中求证△ADE∽△ABC是解题的关键.

练习册系列答案
相关题目
14.关于函数y=-x-2的图象,有如下说法:
①图象过点(0,-2)
②图象与x轴的交点是(-2,0)
③由图象可知y随x的增大而增大
④图象不经过第一象限
⑤图象是与y=-x+2平行的直线,
其中正确说法有( )
①图象过点(0,-2)
②图象与x轴的交点是(-2,0)
③由图象可知y随x的增大而增大
④图象不经过第一象限
⑤图象是与y=-x+2平行的直线,
其中正确说法有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
12. 如图所示,AB∥CD,∠E=26°,∠C=58°,则∠EAB的度数为( )
如图所示,AB∥CD,∠E=26°,∠C=58°,则∠EAB的度数为( )
 如图所示,AB∥CD,∠E=26°,∠C=58°,则∠EAB的度数为( )
如图所示,AB∥CD,∠E=26°,∠C=58°,则∠EAB的度数为( )| A. | 84° | B. | 82° | C. | 79° | D. | 96° |
13.平行四边形ABCD中对角线AC和BD交于点O,AC=6,BD=8,平行四边形ABCD较大的边长是m,则m取值范围是( )
| A. | 2<m<14 | B. | 1<m<7 | C. | 5<m<7 | D. | 2<m<7 |
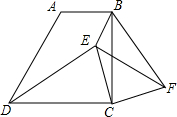 在梯形ABCD中AB∥CD,∠BCD=90°,AB=1,BC=2,tan∠ADC=2.
在梯形ABCD中AB∥CD,∠BCD=90°,AB=1,BC=2,tan∠ADC=2.