题目内容
13．解下列一元二次方程（1）7x（5x+2）=6（5x+2）
（2）4x2-8x+1=0．
分析 （1）方程移项后，利用因式分解法求出解即可；
（2）方程利用公式法求出解即可．
解答 解：（1）方程整理得：7x（5x+2）-6（5x+2）=0，
分解因式得：（7x-6）（5x+2）=0，
解得：x1=$\frac{6}{7}$，x2=-$\frac{2}{5}$；
（2）这里a=4，b=-8，c=1，
∵△=64-16=48，
∴x=$\frac{8±4\sqrt{3}}{8}$=$\frac{2±\sqrt{3}}{2}$，
解得：x1=$\frac{2+\sqrt{3}}{2}$，x2=$\frac{2-\sqrt{3}}{2}$．
点评 此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
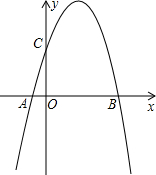如图，在平面直角坐标系中，抛物线y=a2x+bx+4与x轴交于A、B两点（点A在原点左侧，点B在原点右侧），与y轴交于点C．已知OA=1，OC=OB．
8．
如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（ ）
如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（ ）| A． | 34° | B． | 56° | C． | 66° | D． | 54° |
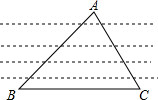如图，为了测量河宽，在河的一边沿岸边选取B、C两点，在对岸岸边选择点A．测得∠B=45°，∠C=60°，BC=30米．求这条河的宽度（这里指点A到直线BC的距离）．（结果精确到1米，参考数据$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）
5．若多项式x2+2ax+4能用完全平方公式进行因式分解，则a值为（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | ±4 |