题目内容
3.一列火车匀速行驶,经过一条长300米的隧道需要20秒的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒.求这列火车的长度.小冉根据学习解决应用问题的经验对上面问题进行了探究,下面是小冉的探究过程,请补充完成:
设这列火车的长度是x米,那么
(1)从车头经过灯下到车尾经过灯下,火车所走的路程是x米,这段时间内火车的平均速度是$\frac{x}{10}$米/秒;
(2)从车头进入隧道到车尾离开隧道,火车所走的路程是(x+300)米,这段时间内火车的平均速度是$\frac{x+300}{20}$米/秒;
(3)火车经过灯下和火车通过隧道的平均速度的关系是相等;
(4)由此可以列出方程并求解出这列火车的长度(请列方程求解)
分析 (1)根据火车长度为xm,根据题意列出代数式即可;
(2)根据题意列出代数式即可;
(3)上述问题中火车的平均速度不发生变化;
(4)根据速度相等列出方程,求出方程的解即可得到结果.
解答 解:(1)根据题意得:从车头经过灯下到车尾经过灯下火车所走的路程为xm,
这段时间内火车的平均速度$\frac{x}{10}$m/s.
故答案为:x,$\frac{x}{10}$;
(2)从车头进入隧道到车尾离开隧道火车所走的路程为(x+300)m,
这段时间内火车的平均速度为$\frac{x+300}{20}$m/s.
故答案为:(x+300);$\frac{x+300}{20}$;
(3)速度没有发生变化,即火车经过灯下和火车通过隧道的平均速度的关系是相等.
故答案为:相等;
(4)根据题意得:$\frac{x}{10}$=$\frac{x+300}{20}$,
解得:x=300.
答:这列火车的长度300m.
点评 本题考查了一元一次方程的应用,解答本题注意理解“完全通过”的含义,完全通过:火车所走的路程=隧道长度+火车长度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.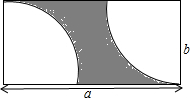 如图所示,阴影部分的面积是(其中a>2b)( )
如图所示,阴影部分的面积是(其中a>2b)( )
 如图所示,阴影部分的面积是(其中a>2b)( )
如图所示,阴影部分的面积是(其中a>2b)( )| A. | ab-$\frac{π{a}^{2}}{4}$ | B. | ab-$\frac{π{b}^{2}}{2}$ | C. | ab-$\frac{π{a}^{2}}{2}$ | D. | ab-$\frac{π{b}^{2}}{4}$ |
18.三角形两边的长分别是4和3,第三边的长是一元二次方程x2-6x+5=0的一个实数根,则该三角形的周长是( )
| A. | 8 | B. | 10 | C. | 12 | D. | 8或12 |
 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,6)的对应点A′的坐标是(6,2).
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,6)的对应点A′的坐标是(6,2).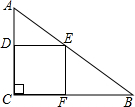 如图,正方形CDEF内接于Rt△ABC,点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时,正方形CDEF的面积是6.
如图,正方形CDEF内接于Rt△ABC,点D、E、F分别在边AC、AB和BC上,当AD=2,BF=3时,正方形CDEF的面积是6.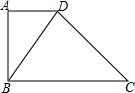 如图,已知四边形ABCD中,∠A=90°,AD∥BC.
如图,已知四边形ABCD中,∠A=90°,AD∥BC. 李先生准备在永川某小区内购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李先生提供了以下两种优惠方案:
李先生准备在永川某小区内购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李先生提供了以下两种优惠方案: