��Ŀ����
2��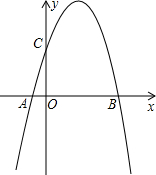 ��ͼ����ƽ��ֱ������ϵ�У�������y=a2x+bx+4��x�ύ��A��B���㣨��A��ԭ����࣬��B��ԭ���Ҳࣩ����y�ύ�ڵ�C����֪OA=1��OC=OB��
��ͼ����ƽ��ֱ������ϵ�У�������y=a2x+bx+4��x�ύ��A��B���㣨��A��ԭ����࣬��B��ԭ���Ҳࣩ����y�ύ�ڵ�C����֪OA=1��OC=OB����1������������ߵĽ���ʽ��
��2������DΪ��һ�������������ϵ�һ�㣬����CD��DB�����ı���OCDB����������ֵ���������ʱD������ꣻ
��3����E�Ǹ���������λ�ڶԳ����Ҳ��һ�����㣬����E��x��ƽ���߽�����������һ��F������E��EH��x���ڵ�H���ٹ���F��FG��x���ڵ�G���õ�����EFGH���ڵ�E���˶������У�������EFGHΪ������ʱ������������εı߳���
���� ��1���������C�����꣬��B�����꼴����ã����ô���ϵ����������������ߵĽ���ʽ��
��2�����D�����꣬������D�����꼴�ɱ�ʾ���ı��ε���������ݺ���������������ֵ����D�����꼴����ã�
��3������E��F���ڶԳ���Գƣ�Ȼ�����������ε����ʼ����з�����⣮
��� �⣺��1����y=a2x+bx+4����x=0����y=4����C�������ǣ�0��4����
��OC=OB��
��B�������ǣ�4��0����
�ѣ�4��0����-1��0��������y=a2x+bx+4�ã�$\left\{\begin{array}{l}{\\;a-\\;b+4=0}\\{16\\;a+4\\;b+4=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{\\;a=-1}\\{\\;b=3}\end{array}\right.$��
�����Ľ���ʽ�ǣ�y=-x2+3x+4��
��2����ֱ��BC�Ľ���ʽ��y=kx+b��
��������ã�$\left\{\begin{array}{l}{4\\;k+\\;b=0}\\{\\;b=4}\end{array}\right.$��
��ã�{��$\left\{\begin{array}{l}{\\;k=-1}\\{\\;b=4}\end{array}\right.$��
��ֱ��BC�Ľ���ʽ��y=-x+4��
��D��m��-m2+3m+4����
��DE��x���ڵ�E��
��S�ı���OCEB=S����OCDE+S��BED=$\frac{1}{2}$��4+��-m2+3m+4����m+$\frac{1}{2}$��4-m����-m2+3m+4��
=-2��m-2��2+14��
��x=2ʱ��y=-2+4=2����D�������ǣ�2��6������ʱS�����ֵ��14��
��3�������ߵĶԳ�����x=$\frac{3}{2}$��
�������εı߳���n����E��������2��$\frac{\\;n}{2}$-$\frac{3}{2}$$\frac{3}{2}$��n����
����y=-x2+3x+4�ã�-��$\frac{\\;n}{2}-\frac{3}{2}$��2+3����$\frac{\\;n}{2}$-$\frac{3}{2}$��+4=n��
��ã�n=4+2$\sqrt{5}$��4-2$\sqrt{5}$����ȥ����
�������ε�����ǣ�4+2$\sqrt{5}$��2=36+16$\sqrt{5}$��
���� ���⿼���˶��κ�����ͼ�������ʣ������ı��ε�������ֵ������ת��Ϊ������ֵ�����ǽ������Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� ��ͼ����O��ֱ��AB��ֱ����CD��������E����A=30�㣬CD=6����Բ�İ뾶��Ϊ��������
��ͼ����O��ֱ��AB��ֱ����CD��������E����A=30�㣬CD=6����Բ�İ뾶��Ϊ��������| A�� | 2$\sqrt{3}$ | B�� | 2 | C�� | 4$\sqrt{3}$ | D�� | $\sqrt{3}$ |

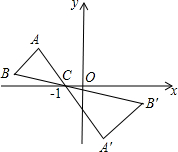 ��ͼ����ABC�У�A��B����������x����Ϸ�����C�������ǣ�-1��0�����Ե�CΪλ�����ģ���x����·�����ABC��λ��ͼ�Ρ�A��B��C�����ѡ�ABC�ı߳��Ŵ�ԭ����2������B��������ǣ�3��-1�������B�������ǣ�-3��$\frac{1}{2}$����
��ͼ����ABC�У�A��B����������x����Ϸ�����C�������ǣ�-1��0�����Ե�CΪλ�����ģ���x����·�����ABC��λ��ͼ�Ρ�A��B��C�����ѡ�ABC�ı߳��Ŵ�ԭ����2������B��������ǣ�3��-1�������B�������ǣ�-3��$\frac{1}{2}$���� ��ͼ�����߶�AB�Ƶ�O˳ʱ����ת90��õ��߶�A��B�䣬��ôA��-2��6���Ķ�Ӧ��A��������ǣ�6��2����
��ͼ�����߶�AB�Ƶ�O˳ʱ����ת90��õ��߶�A��B�䣬��ôA��-2��6���Ķ�Ӧ��A��������ǣ�6��2����