题目内容
将△ABC绕点A顺时针旋转α得到△ADE,DE的延长线与BC相交于点F,连接AF.
(1)如图1,若∠BAC=α=60°,DF=2BF,请直接写出AF与BF的数量关系;
(2)如图2,若∠BAC<α=60°,DF=3BF,猜想线段AF与BF的数量关系,并证明你的猜想;
(3)如图3,若∠BAC<α,DF=mBF(m为常数),请直接写出
的值(用含α、m的式子表示).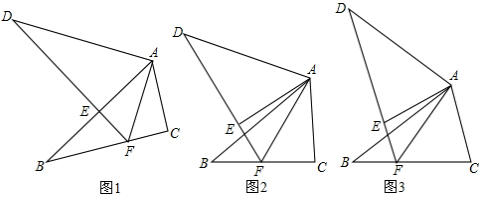
(1)如图1,若∠BAC=α=60°,DF=2BF,请直接写出AF与BF的数量关系;
(2)如图2,若∠BAC<α=60°,DF=3BF,猜想线段AF与BF的数量关系,并证明你的猜想;
(3)如图3,若∠BAC<α,DF=mBF(m为常数),请直接写出
| AF |
| BF |

考点:旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,解直角三角形
专题:
分析:(1)在DF上截取DG=BF,连接AG,根据旋转的性质可得AD=AB,∠D=∠B,然后利用“边角边”证明△ADG和△ABF全等,根据全等三角形对应边相等可得AG=AF,全等三角形对应边相等可得∠DAG=∠BAF,从而求出∠GAF=α,判断出△GAF是等边三角形,再根据等边三角形的三条边都相等可得AF=GF=DG=BF;
(2)求解思路同(1);
(3)在DF上截取DG=BF,连接AG,根据旋转的性质可得AD=AB,∠D=∠B,然后利用“边角边”证明△ADG和△ABF全等,根据全等三角形对应边相等可得AG=AF,全等三角形对应边相等可得∠DAG=∠BAF,从而求出∠GAF=α,判断出△GAF是等腰三角形,并求出GF,过点A作AH⊥DF于H,根据等腰三角形三线合一的性质表示出HF,再利用锐角的正弦列式整理即可得解.
(2)求解思路同(1);
(3)在DF上截取DG=BF,连接AG,根据旋转的性质可得AD=AB,∠D=∠B,然后利用“边角边”证明△ADG和△ABF全等,根据全等三角形对应边相等可得AG=AF,全等三角形对应边相等可得∠DAG=∠BAF,从而求出∠GAF=α,判断出△GAF是等腰三角形,并求出GF,过点A作AH⊥DF于H,根据等腰三角形三线合一的性质表示出HF,再利用锐角的正弦列式整理即可得解.
解答:解:(1)AF=BF.
理由如下:在DF上截取DG=BF,连接AG,(如图1),
由旋转得AD=AB,∠D=∠B,
在△ADG和△ABF中,
,
∴△ADG≌△ABF(SAS),
∴AG=AF,∠DAG=∠BAF,
∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=60°.
∴△GAF是等边三角形,
又∵DF=2BF,
∴AF=GF=DF-DG=DF-BF=BF,
即AF=BF;
(2)解:猜想:AF=2BF.
证明:在DF上截取DG=BF,连接AG(如图2).
由旋转得AD=AB,∠D=∠B,
在△ADG和△ABF中,
,
∴△ADG≌△ABF(SAS),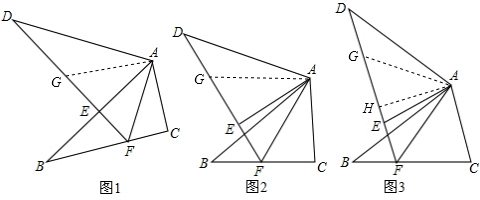
∴AG=AF,∠DAG=∠BAF,
∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=60°,
∴△GAF是等边三角形,
又∵DF=3BF,
∴AF=GF=DF-DG=DF-BF=2BF,
即AF=2BF;
(3)在DF上截取DG=BF,连接AG,(如图3),
由旋转得AD=AB,∠D=∠B,
在△ADG和△ABF中,
,
∴△ADG≌△ABF(SAS),
∴AG=AF,∠DAG=∠BAF,
∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=α,
∴△GAF是等腰三角形,
∵DF=mBF,
∴GF=DF-DG=mBF-BF=(m-1)BF,
过点A作AH⊥DF于H,则FH=
GF=
(m-1)BF,
∠FAH=
∠GAF=
α,
∵sin∠FAH=
,
∴sin
=
,
∴
=
.
理由如下:在DF上截取DG=BF,连接AG,(如图1),
由旋转得AD=AB,∠D=∠B,
在△ADG和△ABF中,
|
∴△ADG≌△ABF(SAS),
∴AG=AF,∠DAG=∠BAF,
∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=60°.
∴△GAF是等边三角形,
又∵DF=2BF,
∴AF=GF=DF-DG=DF-BF=BF,
即AF=BF;
(2)解:猜想:AF=2BF.
证明:在DF上截取DG=BF,连接AG(如图2).
由旋转得AD=AB,∠D=∠B,
在△ADG和△ABF中,
|
∴△ADG≌△ABF(SAS),

∴AG=AF,∠DAG=∠BAF,
∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=60°,
∴△GAF是等边三角形,
又∵DF=3BF,
∴AF=GF=DF-DG=DF-BF=2BF,
即AF=2BF;
(3)在DF上截取DG=BF,连接AG,(如图3),
由旋转得AD=AB,∠D=∠B,
在△ADG和△ABF中,
|
∴△ADG≌△ABF(SAS),
∴AG=AF,∠DAG=∠BAF,
∴∠GAF=∠GAB+∠BAF=∠GAB+∠DAG=∠DAB=α,
∴△GAF是等腰三角形,
∵DF=mBF,
∴GF=DF-DG=mBF-BF=(m-1)BF,
过点A作AH⊥DF于H,则FH=
| 1 |
| 2 |
| 1 |
| 2 |
∠FAH=
| 1 |
| 2 |
| 1 |
| 2 |
∵sin∠FAH=
| FH |
| AF |
∴sin
| α |
| 2 |
| ||
| AF |
∴
| AF |
| BF |
| m-1 | ||
2sin
|
点评:本题考查了全等三角形的性质,等边三角形的性质,解直角三角形,作辅助线构造出全等三角形是解题的关键,此类题目,解题的关键在于前后小题利用的求解思路相同.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
若函数y=mx2+(m+2)x+
m+1的图象与x轴只有一个交点,那么m的值为( )
| 1 |
| 2 |
| A、0 | B、0或2 |
| C、2或-2 | D、0,2或-2 |
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
 在平面直角坐标系xOy中,已知抛物线y=x2-2mx+m2-9.
在平面直角坐标系xOy中,已知抛物线y=x2-2mx+m2-9.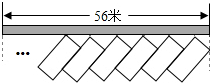 为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出
为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出